Hola Josefina,
En el caso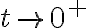 me comí el
me comí el 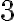 sí. En el otro caso, los términos de orden
sí. En el otro caso, los términos de orden  en
en  del denominador no quedan
del denominador no quedan  en el límite, porque se cancela con la
en el límite, porque se cancela con la  que está dividiendo. El resultado de ese límite es
que está dividiendo. El resultado de ese límite es 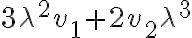 si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a
si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a  , tenemos una indeterminación y hay que resolverla, en este caso cancelando la
, tenemos una indeterminación y hay que resolverla, en este caso cancelando la  en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de
en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de 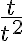 , que si hicieramos ese procedimiento el límite nos daría
, que si hicieramos ese procedimiento el límite nos daría  , pero no existe.
, pero no existe.
Saludos,
Leandro
En el caso
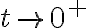 me comí el
me comí el 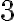 sí. En el otro caso, los términos de orden
sí. En el otro caso, los términos de orden  en
en  del denominador no quedan
del denominador no quedan  en el límite, porque se cancela con la
en el límite, porque se cancela con la  que está dividiendo. El resultado de ese límite es
que está dividiendo. El resultado de ese límite es 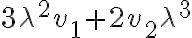 si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a
si no me equivoco. Cuando tenés un cociente donde tanto nominador como denominador tienen a  , tenemos una indeterminación y hay que resolverla, en este caso cancelando la
, tenemos una indeterminación y hay que resolverla, en este caso cancelando la  en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de
en los distintos sumandos. Un ejemplo concreto de ese tipo de error es con el límite de 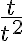 , que si hicieramos ese procedimiento el límite nos daría
, que si hicieramos ese procedimiento el límite nos daría  , pero no existe.
, pero no existe. Saludos,
Leandro
