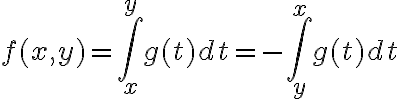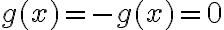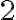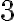Buenas, no entiendo porque la iii y la iv son verdaderas, en la iii supongo que como esta derivando el resultado de derivar una integral es la función misma, pero no entiendo porque el signo de menos. En la iv, se supone que no hay maximos ni minimos porque la función no es acotada?
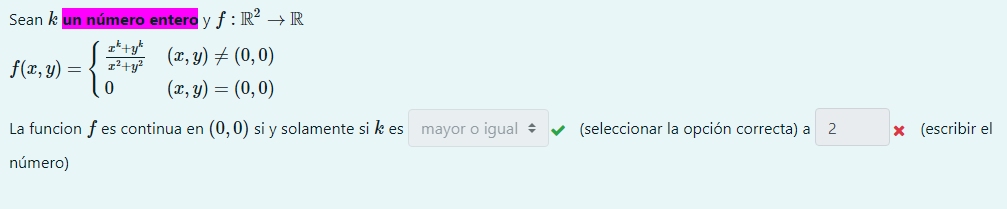
Después en el ejercicio de averiguar k, me dio estos valores, pero nose porque estarían mal