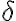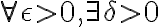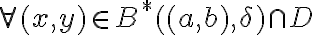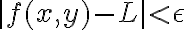Hola, entiendo que al factorizar la funcion f(x,y), el limite me daria 3/2, pero conceptualmente, no estaria mal? dejo foto de lo que hice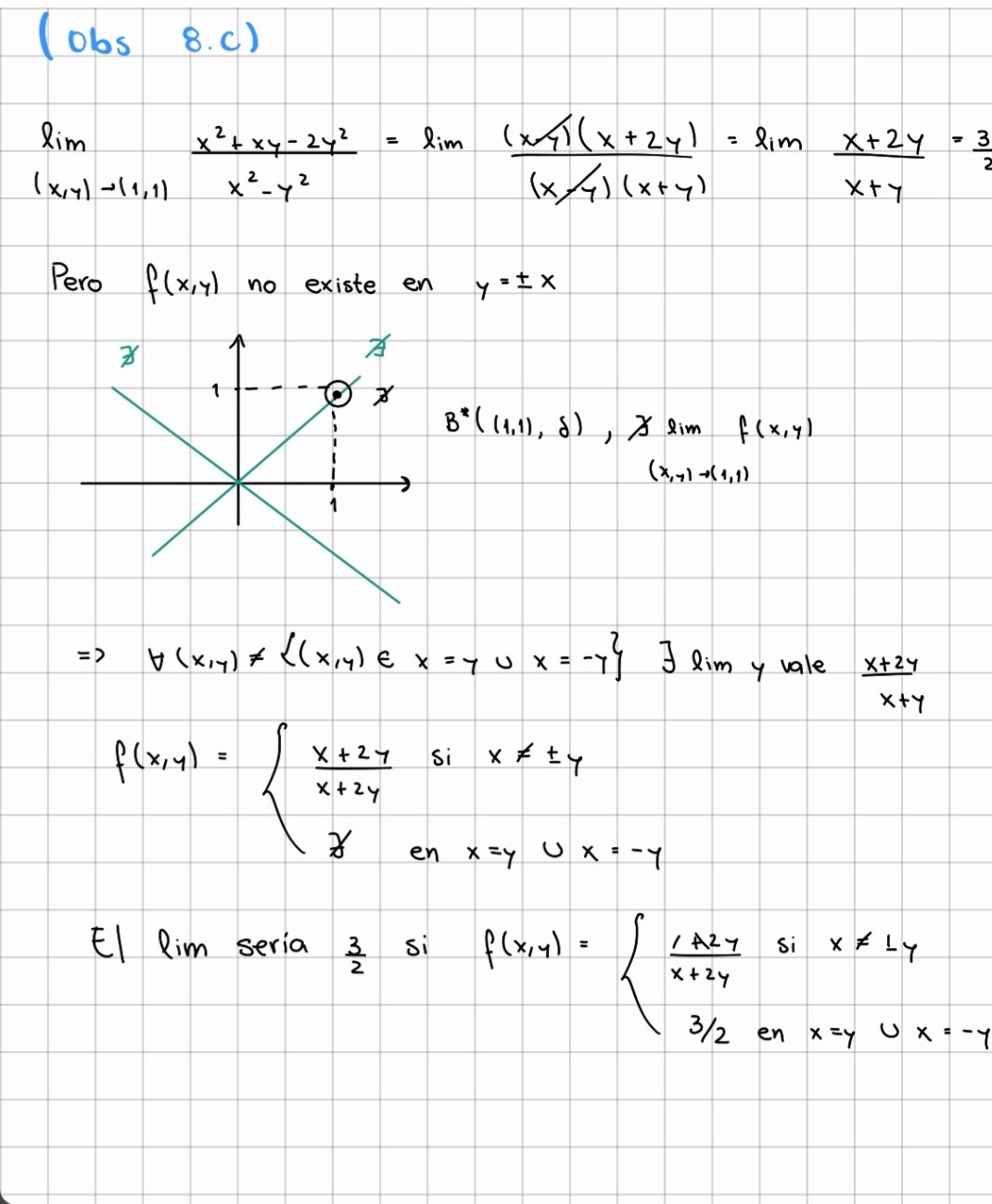 
Hola Milena,
Como dijiste el dominio máximo de la función es el plano menos las rectas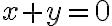
y 
, y 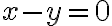como dedujiste la función toma los valores 
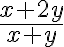para cada punto 
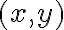del dominio. Para calcular el límite precisamos que el punto donde lo estamos calculando sea un punto de acumulación del dominio, de hecho en todos los otros casos del ejercicio 8 estamos calculando límites en puntos fuera del dominio. Tal vez si me comentás más específicamente qué es lo que te parece mal o contra intuitivo pueda darte una respuesta más precisa que te ayude.
Saludos,
Leandro
Como dijiste el dominio máximo de la función es el plano menos las rectas
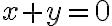y 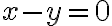, y como dedujiste la función toma los valores 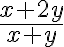para cada punto 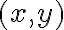del dominio. Para calcular el límite precisamos que el punto donde lo estamos calculando sea un punto de acumulación del dominio, de hecho en todos los otros casos del ejercicio 8 estamos calculando límites en puntos fuera del dominio. Tal vez si me comentás más específicamente qué es lo que te parece mal o contra intuitivo pueda darte una respuesta más precisa que te ayude.Saludos,
Leandro
La condición necesaria para que exista el límite en el punto es que la función exista en una bola B(r, delta) con delta tan pequeño como yo quiera, este caso el punto (1,1) no existe en la recta x=y (punto de no existencia) entonces, no se cumpliría la condición necesaria, porque no existe un delta lo suficientemente pequeño para que todos los puntos pertenezcan a la bola de centro (1,1) y radio delta
Ahora sí entiendo mejor. La definición de límite la bola de centro 
se intersecta con el dominio, dado que no tiene sentido evaluar la función en puntos fuera del dominio, por lo que se pide es que 
tal que 
se cumple que 
.
se intersecta con el dominio, dado que no tiene sentido evaluar la función en puntos fuera del dominio, por lo que se pide es que tal que se cumple que .