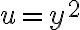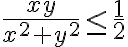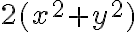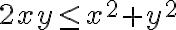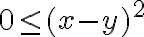Hola, en este ejercicio no entiendo como darme cuenta que la función es menos o igual a 1/2. A mi me quedó el limite de
y. xy´2/x´2+y´4. Yo llegué a la conclusión que es acotado porque cuando x toma valores negativos, la función nunca va a ser menor a -1 ni mayor a 0 y cuando x toma valores positivos, la función no va a ser mayor a 1 ni menor a 0 pero no se como llegar a la que menor o igual a 1/2