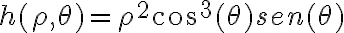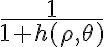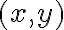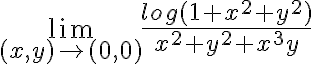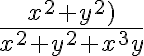Buenas, sobre la parte c tengo la siguiente duda. Llegué que el limite es 0 por cambio de variable a polares, pero ¿eso es suficiente para afirmar que el límite existe y da 0? O en este caso solo sería un candidato, como en el caso de los limites direccionales. En el caso de que me de la información de ser candidato, ya sea para polares o para limites direccionales, como es que termino de probar que el limite existe?
Luego en la parte d, haciendo la equivalencia llego al limite de 1/(x+y), ¿por qué no existe el límite? Pensé que daba infinito. En el e me pasa lo mismo.
Mando foto para que me ayuden a reconocer que estoy razonando mal.