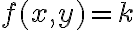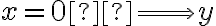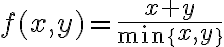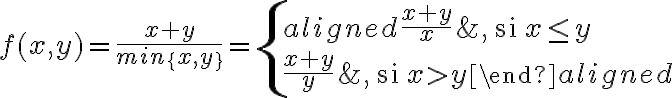Hola, en este ejercicio no se que parte de mi razonamiento esta mal, pero mis resultados no son los que estan en las soluciones.Adjunto mi razonamiento
Hola Ayelén,
Vas bien en el ejercicio. El dominio lo calculaste bien, no lo explicitaste pero calculás los puntos que están en el complemento, está bueno igual hacer el ejercicio de escribirlo explícitamente. Te recomiendo representar en el plano cuál es la región donde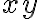 , para luego dibujar la parte del conjunto de nivel correspondiente a cada una. Lo que obtenés ahí es la ecuación de una recta en el plano, no tenemos una variable
, para luego dibujar la parte del conjunto de nivel correspondiente a cada una. Lo que obtenés ahí es la ecuación de una recta en el plano, no tenemos una variable  participando, y luego lo deberías intersectar con la región correspondiente que mencioné antes.
participando, y luego lo deberías intersectar con la región correspondiente que mencioné antes.
Saludos,
Leandro
Vas bien en el ejercicio. El dominio lo calculaste bien, no lo explicitaste pero calculás los puntos que están en el complemento, está bueno igual hacer el ejercicio de escribirlo explícitamente. Te recomiendo representar en el plano cuál es la región donde
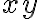 , para luego dibujar la parte del conjunto de nivel correspondiente a cada una. Lo que obtenés ahí es la ecuación de una recta en el plano, no tenemos una variable
, para luego dibujar la parte del conjunto de nivel correspondiente a cada una. Lo que obtenés ahí es la ecuación de una recta en el plano, no tenemos una variable  participando, y luego lo deberías intersectar con la región correspondiente que mencioné antes.
participando, y luego lo deberías intersectar con la región correspondiente que mencioné antes. Saludos,
Leandro
hola, no entiendo por qué calcule los puntos que están en el complemento y no los puntos del conjunto es si. Luego entendí que lo que me quedo en los dos casos que me tome, eran rectas y no planos pero me perdí en la parte donde tengo que intersectar las rectas con las regiones que me quedan separadas por x=y para hallar los conjuntos de nivel. Por qué seria así? Muchas gracias
Hola Leandro, cómo estás?
Podra ser que se suba un desarrollo de como encontrar el conjunto de nivel del ejercicio 2 parte d?
Saludos
Podra ser que se suba un desarrollo de como encontrar el conjunto de nivel del ejercicio 2 parte d?
Saludos
Hola Emanuel,
Tenemos que la función es:
Luego el dominio de  va a ser el dominio de
va a ser el dominio de 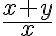 en el semiplano
en el semiplano 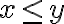 unión el dominio de
unión el dominio de 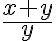 en el semiplano $$y
Al ser una función partida podemos pensarlo como dos funciones definidas en regiones distintas y calcular el dominio y conjuntos de nivel para cada caso correspondiente. De lo enunciado más arriba despejás las ecuaciones y ya tenés los conjuntos buscados.
en el semiplano $$y
Al ser una función partida podemos pensarlo como dos funciones definidas en regiones distintas y calcular el dominio y conjuntos de nivel para cada caso correspondiente. De lo enunciado más arriba despejás las ecuaciones y ya tenés los conjuntos buscados.
Saludos,
Leandro
 va a ser el dominio de
va a ser el dominio de 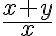 en el semiplano
en el semiplano 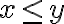 unión el dominio de
unión el dominio de 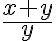 en el semiplano $$y
Al ser una función partida podemos pensarlo como dos funciones definidas en regiones distintas y calcular el dominio y conjuntos de nivel para cada caso correspondiente. De lo enunciado más arriba despejás las ecuaciones y ya tenés los conjuntos buscados.
en el semiplano $$y
Al ser una función partida podemos pensarlo como dos funciones definidas en regiones distintas y calcular el dominio y conjuntos de nivel para cada caso correspondiente. De lo enunciado más arriba despejás las ecuaciones y ya tenés los conjuntos buscados.Saludos,
Leandro
Muchísimas gracias profe! Quedo clarísimo!