Ej 8-b

Ej 8-b

de Tomas Galli Alterwain -
Número de respuestas: 5

Buenas. Estuve intentando resolver este ejercicio, utilicé la notación polar y llegué a una indeterminación, donde r tiende a 0:

r^2/1/log(r.sin \theta)

Hay manera de resolver esa indeterminacion o es mejor tomar otro camino?

Desde ya, muchas gracias.
En respuesta a Tomas Galli Alterwain

Re: Ej 8-b

de Veronica Rumbo -

Hola Tomás. En primer lugar quiero decir que no me queda claro cómo llegaste a esa expresión en coordenadas polares (hago el cambio de coordenadas y me da otra cosa).

De todos modos, en este caso no es necesario hacer el cambio de coordenadas. Mi sugerencia es que notes que el límite que estás estudiando lo podés escribir como producto de dos factores: uno acotado en la región cercana al origen (por ejemplo x) y el otro que tiende a cero (por ejemplo y \log(y).

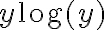Lo cómodo de esta descomposición es que en ambos factores por separado hay una variable sola por lo que al calcular los límites estás trabajando con funciones de una variable, un terreno que nos es bastante más familiar. No todas las funciones nos permiten esta factorización tan conveniente, pero ya que acá se puede, aprovechemos.

Saludos.
En respuesta a Veronica Rumbo

Re: Ej 8-b

de Alexis Sokorov Vargas -
Buenas noches, tengo una duda respecto a cómo evaluar el \lim y es que ¿cómo sé el comprtamiento de y \ln(|y|) ? Porque y \rightarrow 0 y \ln(|y|) \rightarrow - \infty entonces no comprendo muy bien cómo es la mano, independientemente de que x \rightarrow 0 .
¿Sería 0 por algo que también tiende a 0 ?
O puede que lo siguiente sea una equivalencia:
\lim_{y\to 0} y \ln(y) = \lim_{y\to \infty} \frac{1}{y} \ln( \frac{1}{y} ) entonces, por órdenes, \frac{1}{y} \rightarrow 0 más rápido de lo que \ln \rightarrow - \infty
En respuesta a Alexis Sokorov Vargas

Re: Ej 8-b

de Leandro Bentancur -
Buenas noches Alexis,
Es una indeterminación pero sale por órdenes sí. Una forma de verlo es que ylog(y)=\frac{log(y)}{\frac{1}{y}}.
Saludos,
Leandro
En respuesta a Leandro Bentancur

Re: Ej 8-b

de Zoé Castro Brando -
Buenas, sigo sin notar realmente por qué el 1/y tiene mas rapido a 0 que el logaritmo a -infinito, entiendo que se resuelve la indeterminación por ordenes, pero no veo realmente como pensarlo. Lo que tengo entendido es que en infinito los ordenes son log (x) menor a x menor a x potencia menor a numero a la x.