Hola Francisco,
Para calcular la integral de segunda especie en el intervalo ![[1,2] [1,2]](https://eva.fing.edu.uy/filter/tex/pix.php/f79408e5ca998cd53faf44af31e6eb45.gif) primero podemos observar que
primero podemos observar que 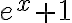 no se anula y es acotada en ese intervalo, por lo que la integral es equivalente a
no se anula y es acotada en ese intervalo, por lo que la integral es equivalente a 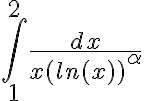 . Para calcular esta integral podemos hacer el cambio de variable
. Para calcular esta integral podemos hacer el cambio de variable 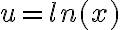 y
y 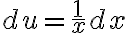 .
.
Otra forma es usar que  en ese intervalo tampoco se anula y es acotada, para calcular entonces si converge la integral
en ese intervalo tampoco se anula y es acotada, para calcular entonces si converge la integral  , y allí usar el equivalente en
, y allí usar el equivalente en  de
de  .
.
Saludos,
Leandro
