Buenas, no entiendo como trabajar con la sucesión para demostrar si es decreciente o creciente, ¿Cómo se tendría que hacer?

Buenas, no entiendo como trabajar con la sucesión para demostrar si es decreciente o creciente, ¿Cómo se tendría que hacer?

Buenas!
Para estudiar la monotonía estudiamos la inecuación 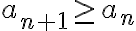 :
:
Por lo tanto, estudiando el signo de la inecuación anterior llegamos a la conclusión de que la sucesión es creciente sii ![a_n \in [ -1-\sqrt{2},-1+\sqrt{2} ] a_n \in [ -1-\sqrt{2},-1+\sqrt{2} ]](https://eva.fing.edu.uy/filter/tex/pix.php/6e578e5d5dc7de807f501f6af1c7b90d.gif) mientras que será decreciente sii
mientras que será decreciente sii 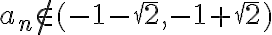 .
.
Para terminar falta ver cuando se encuentra en estos intervalos.
Si el límite existe pueden suceder 2 cosas, la primera que sea infinito y la segunda que sea finito.
Suponemos que es infinito, entonces se tiene que cumplir que 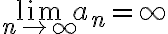 pero:
pero:
Ese límite también debería ser infinito por lo que si existe, el límite de la sucesión debe ser finito. Nos paramos en este caso y asumimos que dicho límite vale  , entonces tenemos que:
, entonces tenemos que:
Por lo que el límite existe y es finito, si 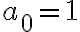 entonces nos encontramos en la zona donde la sucesión es decreciente y por lo tanto el límite es
entonces nos encontramos en la zona donde la sucesión es decreciente y por lo tanto el límite es 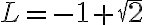 , pero por la desigualdad habíamos obtenido que en esta zona es simplemente decreciente por lo que la opción C no nos sirve.
, pero por la desigualdad habíamos obtenido que en esta zona es simplemente decreciente por lo que la opción C no nos sirve.
Luego si 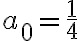 entonces partimos de la zona donde la sucesión es creciente y con límite
entonces partimos de la zona donde la sucesión es creciente y con límite 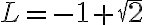 por lo que la opción correcta es la D.
por lo que la opción correcta es la D.
Saludos!
Florencia
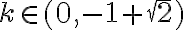 entonces los términos de la sucesión siempre permanecerán en ese intervalo, y lo mismo pasa con el intervalo
entonces los términos de la sucesión siempre permanecerán en ese intervalo, y lo mismo pasa con el intervalo 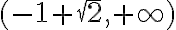 .
.