Hola Josefina,
Para el ejercicio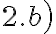 la idea es seguir los mismos pasos que en el
la idea es seguir los mismos pasos que en el  . Para calcular el límite tenemos que usar que si existe el límite y es
. Para calcular el límite tenemos que usar que si existe el límite y es  , entonces debe cumplir que
, entonces debe cumplir que 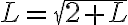 . Esto es que sea un punto fijo de la función
. Esto es que sea un punto fijo de la función 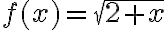 .
.
Para el te recomiendo pensar cuál es la mayor cantidad de factores primos que puede tener un número
te recomiendo pensar cuál es la mayor cantidad de factores primos que puede tener un número  . Por ejemplo, un número
. Por ejemplo, un número  no puede tener
no puede tener  factores
factores 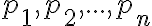 porque sabemos que
porque sabemos que  (donde usamos que cada primo es mayor o igual a
(donde usamos que cada primo es mayor o igual a 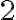 ). La idea es acotar
). La idea es acotar 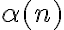 por algo que luego sepas calcular el límite
por algo que luego sepas calcular el límite 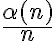 .
.
Para el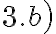 , cada término de la sucesión está en la variable
, cada término de la sucesión está en la variable 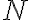 . Por ejemplo
. Por ejemplo 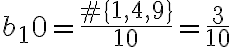 y
y 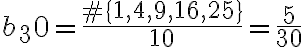 .
.
Para el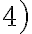 . Es la definición de función no acotada exacto. Para la parte
. Es la definición de función no acotada exacto. Para la parte 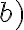 ,no es necesario que la función sea monótona. La idea es que como sabés que para todo
,no es necesario que la función sea monótona. La idea es que como sabés que para todo  existe un punto
existe un punto 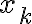 tal que
tal que 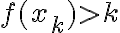 , podés usar esa como sucesión.
, podés usar esa como sucesión.
Saludos,
Leandro
Para el ejercicio
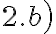 la idea es seguir los mismos pasos que en el
la idea es seguir los mismos pasos que en el  . Para calcular el límite tenemos que usar que si existe el límite y es
. Para calcular el límite tenemos que usar que si existe el límite y es  , entonces debe cumplir que
, entonces debe cumplir que 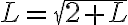 . Esto es que sea un punto fijo de la función
. Esto es que sea un punto fijo de la función 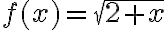 .
.Para el
 te recomiendo pensar cuál es la mayor cantidad de factores primos que puede tener un número
te recomiendo pensar cuál es la mayor cantidad de factores primos que puede tener un número  . Por ejemplo, un número
. Por ejemplo, un número  no puede tener
no puede tener  factores
factores 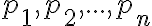 porque sabemos que
porque sabemos que  (donde usamos que cada primo es mayor o igual a
(donde usamos que cada primo es mayor o igual a 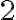 ). La idea es acotar
). La idea es acotar 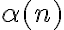 por algo que luego sepas calcular el límite
por algo que luego sepas calcular el límite 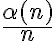 .
.Para el
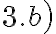 , cada término de la sucesión está en la variable
, cada término de la sucesión está en la variable 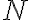 . Por ejemplo
. Por ejemplo 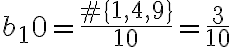 y
y 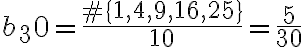 .
.Para el
 . Es la definición de función no acotada exacto. Para la parte
. Es la definición de función no acotada exacto. Para la parte  ,no es necesario que la función sea monótona. La idea es que como sabés que para todo
,no es necesario que la función sea monótona. La idea es que como sabés que para todo  existe un punto
existe un punto 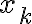 tal que
tal que 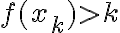 , podés usar esa como sucesión.
, podés usar esa como sucesión.Saludos,
Leandro
