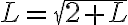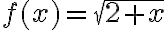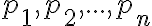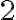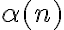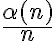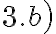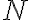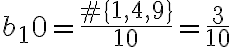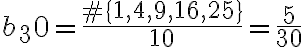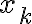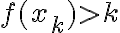Buenas, quería consultar a cerca de algunos de los ejercicios complementarios ya que no están en las soluciones del practico.
Primero, quería saber en el ejercicio 2b), cómo estudiar el limite de una sucesión definida por recurrencia. En este caso tengo que mi elemento an es la raíz de 2 + an-1, entonces en el limite de an me aparece an-1, el cual de vuelta calculo su valor por recurrencia y seria imposible calcular an en el infinito.
Ademas, me gustaría consultar cómo encarar el ejercicio 3.a). Yo había pensado en que al descomponer un numero en sus factores primos, es 1 factor si el numero es primo, en cuyo caso la sucesión tomara el valor de 1/n, o tiene mas que un factor, pero menos que n factores, en cuyo caso an es menor que 1. Igualmente, no llega un punto donde los números son o todos primos o todos compuestos, con lo que pensé que an es una sucesión que oscila, por lo que no puede converger. No se si mi razonamiento es correcto, o si en realidad si converge.
Luego, para el 3b) no comprendo los valores que toma la sucesión, si es que fija un n y hace variar a N.
Por ultimo, para el ejercicio 4: en el 4a) queria saber si la "negación de acotación de una función" se refiere simplemente a la definición de una sucesión no acotada y en el 4b) como puedo construir una sucesión que haga que f(an) sea monótona creciente para afirmar que el limite es infinito.
Desde ya muchas gracias.