Buenas, quería saber si esta demostración estaría correcta?
Muchas gracias. Saludos!
Sí, está muy bien. Tanto la idea a gran escala como la forma de escribirla. Felicitaciones!
Genial, muchas gracias!
En respuesta a Veronica Rumbo
Re: Ejercicio 8, práctico 3
Buenas, estaba viendo como habian hecho el ejercicio 8, y me queda todo claro excepto el por que eligio especificamente epsilon = K - L. Como se de antemano que ese epsilon es conveniente para mi demostracion?
Saludos
En respuesta a Emiliano Benjamin Guarteche Pastorino
Re: Ejercicio 8, práctico 3
de Marcos Dura Sosa -
Hola Emiliano,
Elige epsilon = L - K, no K - L.
No soy profe, pero entiendo que es porque vos estas buscando demostrar que efectivamente L = K, entonces te conviene elegir ese epsilon que a priori > 0 para luego llegar al absurdo de que no es posible que L > K y que tienen que ser iguales.
Quizas un profe pueda explicartelo mejor.
Elige epsilon = L - K, no K - L.
No soy profe, pero entiendo que es porque vos estas buscando demostrar que efectivamente L = K, entonces te conviene elegir ese epsilon que a priori > 0 para luego llegar al absurdo de que no es posible que L > K y que tienen que ser iguales.
Quizas un profe pueda explicartelo mejor.
Hola a ambos,
Está correcto lo que dice Marcos. Agrego además que lo que se está buscando es que por un lado por la definición de supremo no va a haber valores de la sucesión en el intervalo![(K, L]](https://eva.fing.edu.uy/filter/tex/pix.php/451067fdcdb027fba4390a7e7e08c0d7.png "(K, L]")
(el segmento marcado con rojo y que es de tamaño 
), pero por otro lado si el límite de la sucesión es 
si los debe haber, llegando a una contradicción. De esa idea es que sale esa elección del epsilon.
Saludos,
Leandro
Está correcto lo que dice Marcos. Agrego además que lo que se está buscando es que por un lado por la definición de supremo no va a haber valores de la sucesión en el intervalo
(el segmento marcado con rojo y que es de tamaño 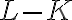), pero por otro lado si el límite de la sucesión es si los debe haber, llegando a una contradicción. De esa idea es que sale esa elección del epsilon.Saludos,
Leandro
Buenas! Hay una parte de la demostración en la resolución del práctico que no entiendo para nada
Me podrían explicar de dónde sale eso??
Dado n natural existe un valor x perteneciente a a tal que la distancia entre el supremo y x es menor a 1/n? De dónde sale esa afirmación?
Si A = {1,2,3} qué n natural y x perteneciente a A existen tal que |3 - x|< 1/n ? x es una sucesión? Cuál sería en este caso?
Muchas gracias!
Hola Sebastián,
En el ejemplo que das 
sería 
para todo 
.
Si no hubiera ningún elemento de 
en el intervalo ![(L-\frac{1}{n}, L]](https://eva.fing.edu.uy/filter/tex/pix.php/c7110238df05815c3978ee0634f3cf33.png "(L-\frac{1}{n}, L]")
entonces tendríamos una cota superior más chica que . Esa es la justificación para la afirmación resaltada.
Saludos,
Leandro