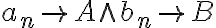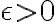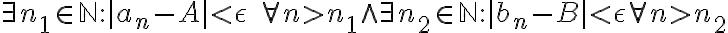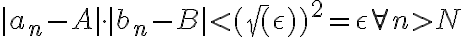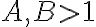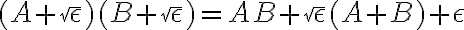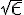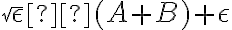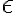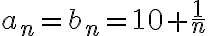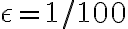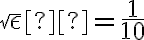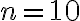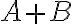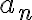 y
y 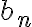 dos sucesiones reales convergentes tales que sus limites son
dos sucesiones reales convergentes tales que sus limites son  y
y  respectivamente: demostrar que
respectivamente: demostrar que 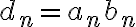 tiene limite
tiene limite 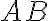 " intenté demostrarlo por mi cuenta antes de ver la solución, y si bien llegue a algo, me serví de un paso que considero "tenebroso", por decirle de alguna manera jajaja. Supongo que esta demostración no es válida, pero me gustaría saber porque exactamente.
" intenté demostrarlo por mi cuenta antes de ver la solución, y si bien llegue a algo, me serví de un paso que considero "tenebroso", por decirle de alguna manera jajaja. Supongo que esta demostración no es válida, pero me gustaría saber porque exactamente. La demostración es la siguiente:
En particular, ambas proposiciones se cumplen para 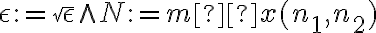
Por propiedad de valor absoluto, el producto de los valores absolutos es el valor absoluto del producto: 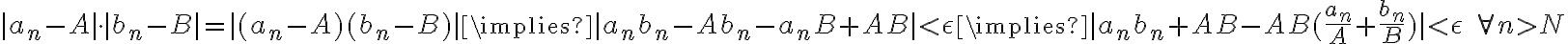
Y el "paso tenebroso", es que como por hipótesis, estamos trabajando a partir de un momento N para el cuál se cumple que tanto 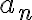 como
como 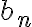 son arbitrariamente cercanos a
son arbitrariamente cercanos a  y
y  respectivamente, asumo que
respectivamente, asumo que 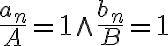 , luego
, luego 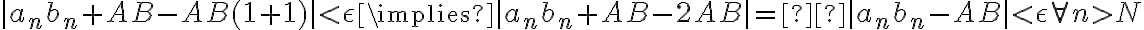
En definitiva, estoy tomando el límite de las fracciones en un entorno arbitrariamente pequeño de los límites y asumiendo entonces que ese cociente da 1, lo cuál dudo que sea "legal", pero es a lo mejor que pude llegar sin recurrir a las ideas felices para factorizar a conveniencia las expresiones. De antemano, noté un problema y es que estaría dividiendo entre cero si cualquiera de los dos límites, A o B fuesen cero, pues por hipótesis, tranquilamente podrían darse esos casos.
Agradezco cualquier comentario respecto a si esto esta bien o esta mal, y si esta mal, si puede modificarse algo para corregirlo. Muchas gracias.