Hola Ayelén,
No me queda claro si estás pensando en el plano o en el espacio. En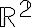 podemos tener una circunsferencia no una esfera, y la ecuación de una recta es de la forma
podemos tener una circunsferencia no una esfera, y la ecuación de una recta es de la forma 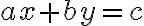 . En
. En 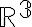 una ecuación de la forma
una ecuación de la forma 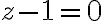 es un plano, no sé si estabas pensando en eso.
es un plano, no sé si estabas pensando en eso.
Podemos pensarlo fijando primero, es decir, ver los puntos que están en un plano de la forma
primero, es decir, ver los puntos que están en un plano de la forma 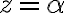 . En ese plano los puntos que van a pertenecer a nuestro conjunto son los que verifican
. En ese plano los puntos que van a pertenecer a nuestro conjunto son los que verifican 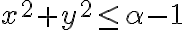 . Aquí tenemos tres casos, si
. Aquí tenemos tres casos, si 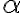 entonces el conjunto es vacío, si
entonces el conjunto es vacío, si 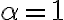 el conjunto es un único punto
el conjunto es un único punto  , y si
, y si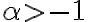 entonces el conjunto es un círculo centrado en el origen y de radio
entonces el conjunto es un círculo centrado en el origen y de radio 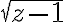 . Ahora si vemos todo el conjunto tenemos un cono cuyo eje de simetría es el eje
. Ahora si vemos todo el conjunto tenemos un cono cuyo eje de simetría es el eje 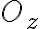 y el radio va aumentando a medida que crece
y el radio va aumentando a medida que crece  .
.
Saludos,
Leandro
No me queda claro si estás pensando en el plano o en el espacio. En
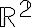 podemos tener una circunsferencia no una esfera, y la ecuación de una recta es de la forma
podemos tener una circunsferencia no una esfera, y la ecuación de una recta es de la forma 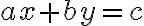 . En
. En 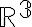 una ecuación de la forma
una ecuación de la forma 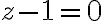 es un plano, no sé si estabas pensando en eso.
es un plano, no sé si estabas pensando en eso.Podemos pensarlo fijando
 primero, es decir, ver los puntos que están en un plano de la forma
primero, es decir, ver los puntos que están en un plano de la forma 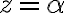 . En ese plano los puntos que van a pertenecer a nuestro conjunto son los que verifican
. En ese plano los puntos que van a pertenecer a nuestro conjunto son los que verifican 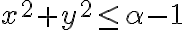 . Aquí tenemos tres casos, si
. Aquí tenemos tres casos, si 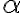 entonces el conjunto es vacío, si
entonces el conjunto es vacío, si 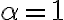 el conjunto es un único punto
el conjunto es un único punto  , y si
, y si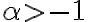 entonces el conjunto es un círculo centrado en el origen y de radio
entonces el conjunto es un círculo centrado en el origen y de radio 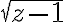 . Ahora si vemos todo el conjunto tenemos un cono cuyo eje de simetría es el eje
. Ahora si vemos todo el conjunto tenemos un cono cuyo eje de simetría es el eje 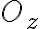 y el radio va aumentando a medida que crece
y el radio va aumentando a medida que crece  .
.Saludos,
Leandro
