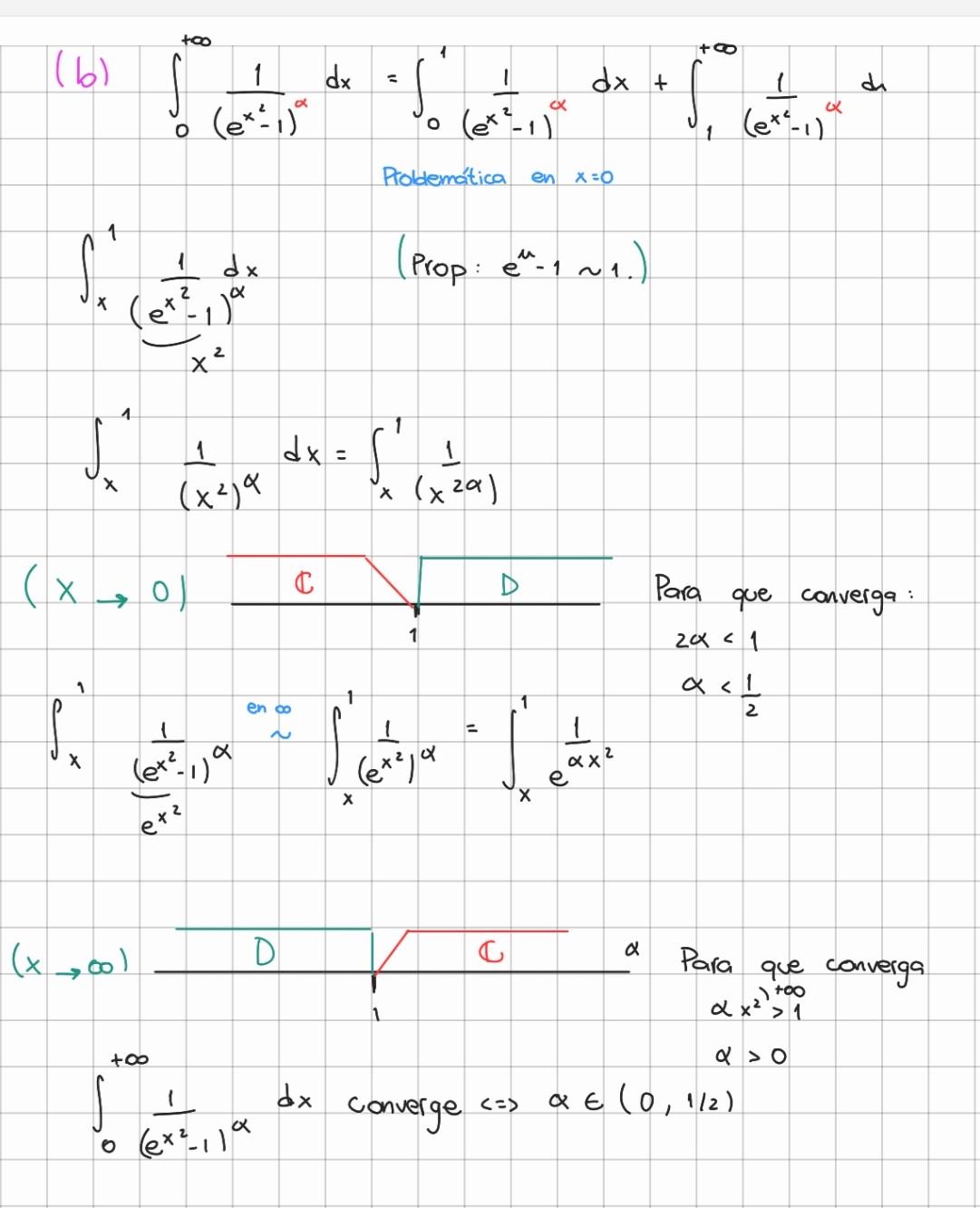
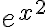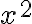Hola!! Tengo una duda porque en el ejercicio 7.b que tenemos que hallar alfa para que la integral impropia sea convergente, cuando x tiende a infinito llego a la expresión 1/e a la alfa por x al cuadrado, y no sabia que hacer para llegar a la expresión 1/x a la alfa y hacer por la regla de convergencia y divergencia dependiendo de el valor de alfa.Vi que una chica lo hacia con esa misma expresión y hallaba el alfa, está bien asi?? pense que era solo para la funcion 1/x a la alfa. Dejo la captura de lo que hice