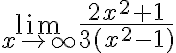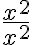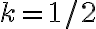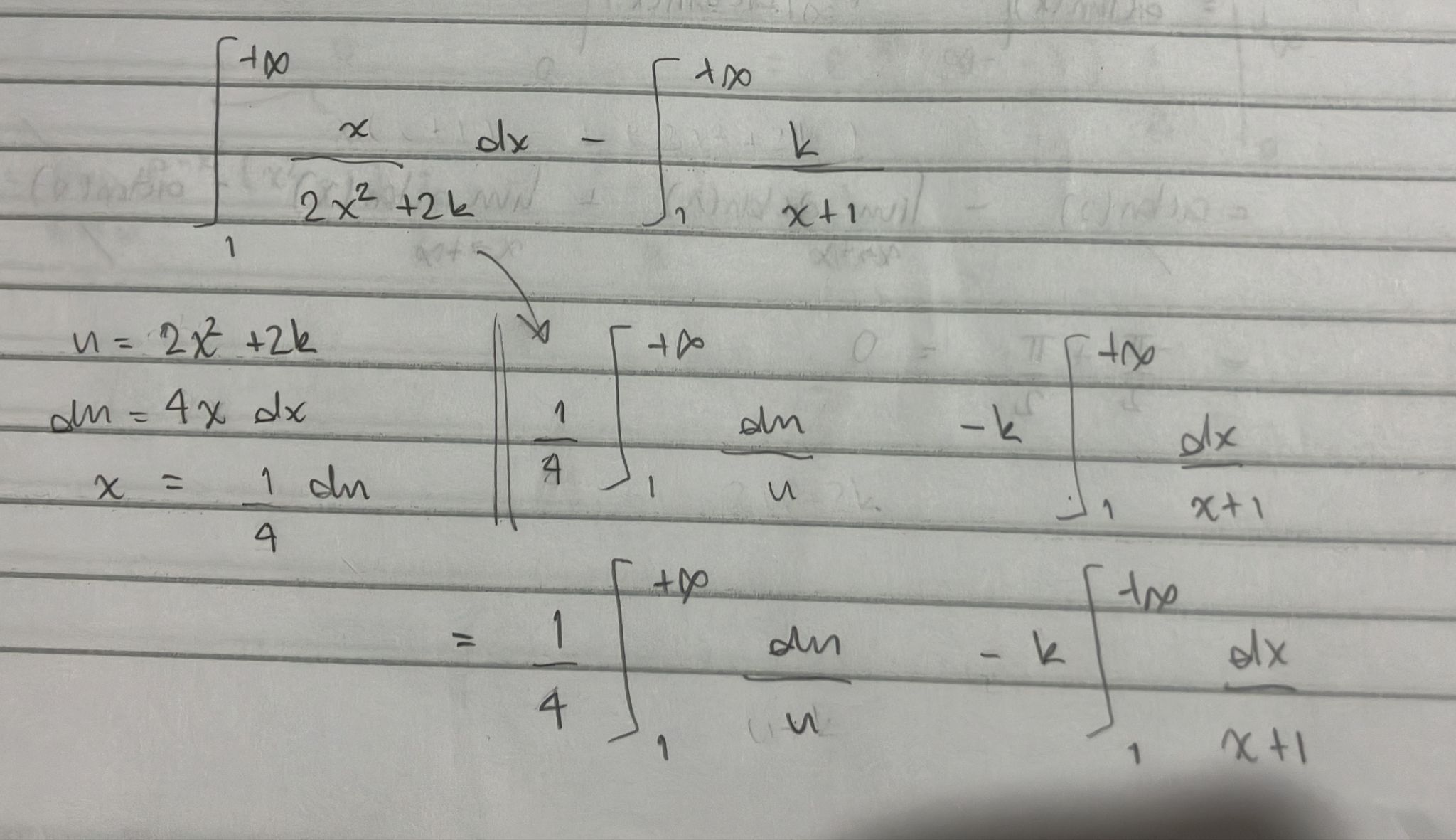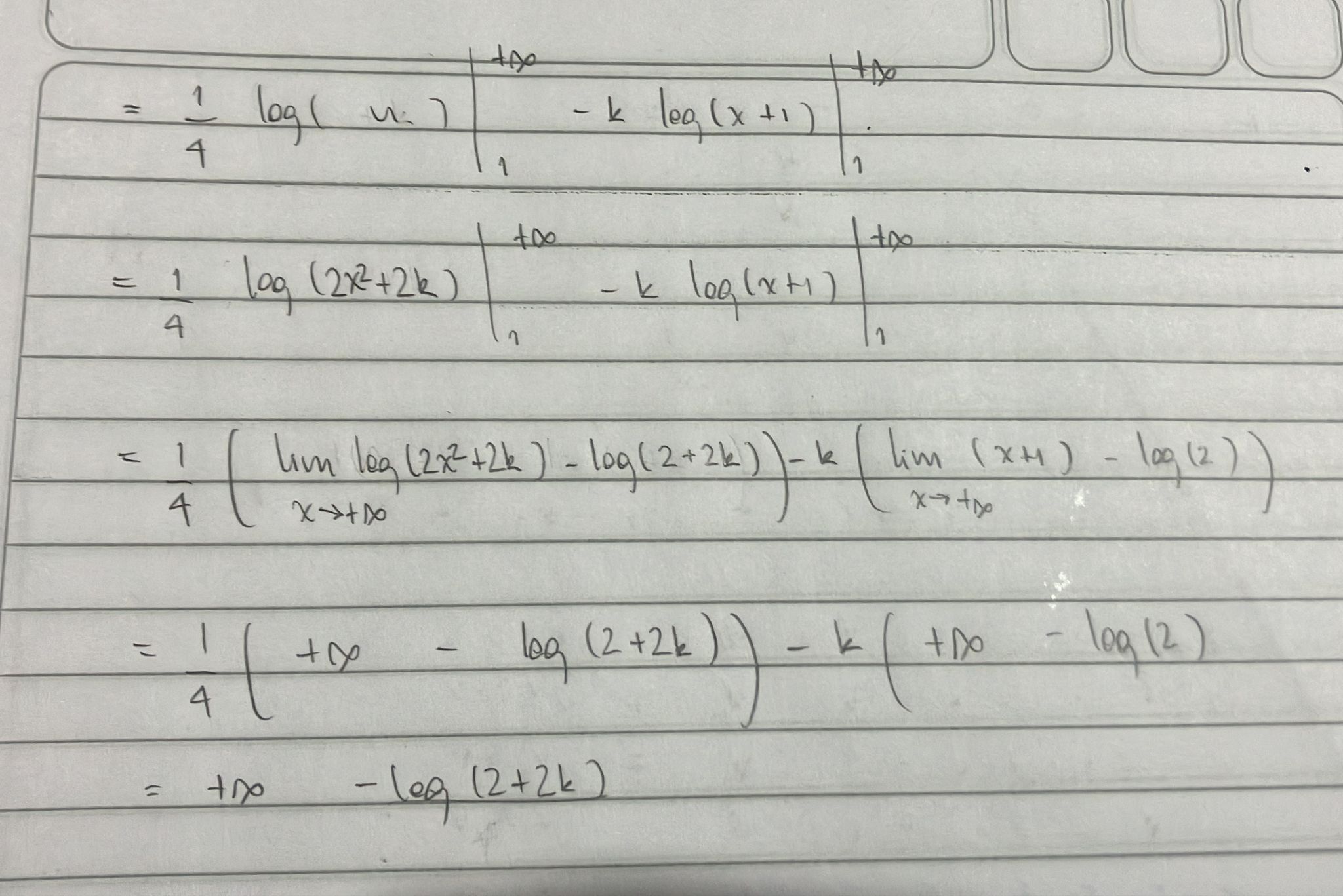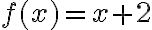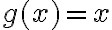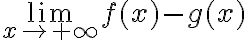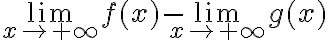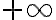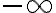Foro Práctico 5

Hola María. El error está cerca del final, cuando usás órdenes de infinitos para simplificar la expresión cuyo límite estás calculando.

Esa simplificación es válida para determinar si es convergente o no (ya que se mantiene la condición de convergente/ divergente). Pero no es cierto que los límites sean literalmente los mismos. Especialmente en el caso que nos compete, que es cuando el límite da una constante finita.

Para explicar mejor, pongamos un ejemplo de juguete, imaginate que estás calculando el límite

$\lim_{x \rightarrow \infty} \frac{2x^2 +1}{3(x^2-1)}$.

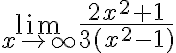A los efectos de determinar si la expresión converge o no, podrías simplificarla mirando los términos de grado mayor (que es lo que vos hiciste en el ejercicio según entiendo), y mirar el límite de 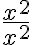$\frac{x^2}{x^2}$. Sin embargo, no es cierto que ambos límites sean iguales, ya que en el primer caso da 2/3 y en el otro da 1.

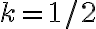La solución al problema, no deshacerse de las constantes tan alegremente. Ahora que ya sabés que el $k$ que nos interesa es 1/2, te sugiero volver un par de pasos atrás en la igualdad -aunque ahora ya tomando $k = 1/2$ y calcular el límite teniendo cuidado con las equivalencias.