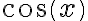Buenas, veo que en la solución para probar la convergencia de la primera integral se aplica un cambio de variable, ¿se puede demostrar por partes también?
Lo hice de la siguiente manera:


Aplicando partes me da que la integral es: 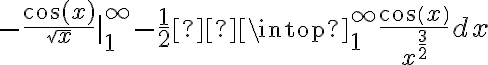
Pregunta: ¿podría aplicar el criterio de convergencia absoluta cuando se trata de 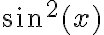 o con
o con 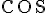 ?
?