Buenas! No logro llegar a la respuesta de este ejercicio. Pude probar que la integral converge si alfa es mayor a 1 pero no encuentro como probar que es convergente si es mayor a 0. Como puedo hacer?

Buenas! No logro llegar a la respuesta de este ejercicio. Pude probar que la integral converge si alfa es mayor a 1 pero no encuentro como probar que es convergente si es mayor a 0. Como puedo hacer?

Hola Julieta,
Tenemos :
La integral del segundo sumando converge porque es una función más chica que 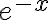 , por lo tanto la convergencia de la suma va a depender de si la integral del primer sumando converge o no. Para eso podemos usar que
, por lo tanto la convergencia de la suma va a depender de si la integral del primer sumando converge o no. Para eso podemos usar que 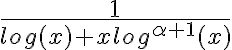 es equivalente a
es equivalente a 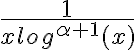 , y estudiar esta última. Fijate si podés estudiar la convergencia de esa integral (es el ej 2a del práctico 5), cualquier cosa me comentás de nuevo por acá.
, y estudiar esta última. Fijate si podés estudiar la convergencia de esa integral (es el ej 2a del práctico 5), cualquier cosa me comentás de nuevo por acá.
Saludos,
Leandro