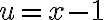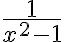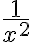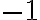CDIVV-2S: 6-h

Buenas tardes, tengo una duda respecto lo siguiente:

Para clasificar la integral hice esto : 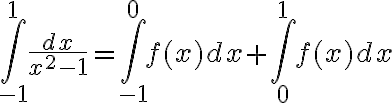$\int_{-1}^{1} \frac{dx}{x^2-1} = \int_{-1}^{0}f(x)dx+\int_{0}^{1}f(x)dx$

Traté de comparar 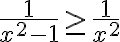$\frac{1}{x^2-1} \geq \frac{1}{x^2}$ y como 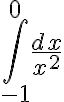$\int_{-1}^{0} \frac{dx}{x^2}$ diverge con 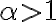$\alpha > 1$ , entonces la integral original diverge.

Porque en las soluciones me dice que en 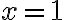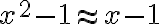$x=1$ , $x^2 - 1 \approx x-1$ , traté de evaluar la integral del último término y me da que no existe si hago cambio de variable $u=x-1$

Re: 6-h

de Leandro Bentancur - miércoles, 13 de septiembre de 2023, 09:46

Hola Alexis,
La desigualdad esa no es cierta,

$\frac{1}{x^2-1}$ es negativa y

$\frac{1}{x^2}$ es positiva. Además la propiedad nos sirve cuando son funciones del mismo signo. Acá tenemos

$\frac{1}{x^2}$ que tiene asíntotas en

$-1$ y

$1$ , por lo que tenemos que buscar funciones que sean más sencillas de integrar (o que ya conozcamos su comportamiento) con las que podamos usar los criterios de comparación o equivalencia, o sea, que tiendan a infinito en alguno de esos dos valores.
Saludos,
Leandro