Hola, clasifique la primera integral ( sen(t^2) ) multiplicando y dividiendo por 2t, usando la proposición de la parte 5a llegue a que converge.
No entiendo como plantean la divergencia de la segunda ( lsen(t^2)l ).
Hola Antonela,
La idea es acotar la integral por abajo con triángulos que sepamos calcular su área. Para esto podemos ver primero un intervalo de la forma ![[\sqrt{k \pi},\sqrt{(k+1) \pi}]](https://eva.fing.edu.uy/filter/tex/pix.php/a4303921be2581d77a1bcc4585d6736b.png "[\sqrt{k \pi},\sqrt{(k+1) \pi}]")
y calcular el área del triángulo con esa base y que pasa por el punto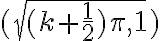 
(que es el punto de la gráfica donde se alcanza el máximo). Ese triángulo te queda debajo de la gráfica, por lo que la integral de la función en ese intervalo es mayor al área del triángulo. Luego utilizando eso podemos llegar al resultado.
Fijate si con esto te sale y sino volvé a comentar nomás.
Saludos,
Leandro
Bien, seguí la idea y llegue a las mismas expresiones de mínimos y máximos para los triángulos. Lo que no me queda claro es como justificar que esa integral "mas chica" diverge para poder aplicar comparación.
Gracias.
Gracias.
La integral de la poligonal va a ser la suma del área de todos los triángulos, es decir, la podés calcular como una serie.