Foro de Teórico

Buen día, tengo una duda respecto a lo siguiente:

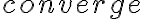para poder determinar la convergencia de la impropia (no pudimos determinarla mediante comparación ya que $n \leq  n\ln(n) \leq n^{\alpha}  \Leftrightarrow \frac{1}{n} \geq \frac{1}{n\ln(n)}\geq \frac{1}{n^{\alpha}}, \alpha > 1$, o sea es más grande que una que $diverge$ pero es más chica que una que $converge$) evaluamos la primitiva 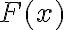$F(x)$ y si nos da que, cuando $x \rightarrow \infty , F(x)=\infty$ la integral converge. Mi duda es la siguiente:

decimos que la serie también converge por esta comparación:¿ 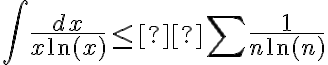$\int \frac{dx}{x\ln(x)} \leq  \sum \frac{1}{n\ln(n)}$ ?