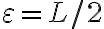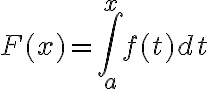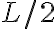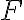CDIVV-2S: Integrales Impropias

Buen día, en las notas del curso se da la siguiente proposición:

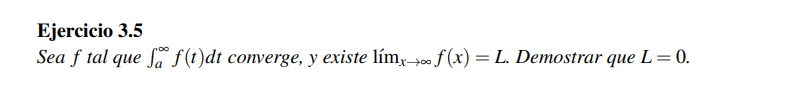
No entiendo cómo atacar este ejercicio. En el teórico hicimos una representación gráfica que ilustra una idea del porqué es así la proposición:

Si el límite $L$ es distinto de $0$ , el área a determinar es infinita, por ende, el límite no puede ser $L \neq 0$

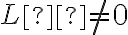
Es decir, una integral impropia finita, su límite no necesariamente es cero. Si agregamos que tiene límite 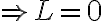$L$ $\Rightarrow L = 0$ . No sabría cómo demostrarlo

Re: Integrales Impropias

de Marcelo Fiori - jueves, 7 de septiembre de 2023, 20:18

Hola Alexis

Como el límite en infinito es L>0, existe un real K tal a partir del cual la función es más grande que L/2 (es decir, tomando

$\varepsilon = L/2$ y aplicando la definición de límite).

Entonces, si querés podés partir la

$F(x) = \int_a^x f(t)dt$ como la siguiente suma:

$F(x) = \int_a^K f(t)dt + \int_K^x f(t)dt$
La primera integral es un número, una constante

$C$ , y usando que

$f$ es más grande que

$L/2$ en la segunda integral, podés acotar

$F$ por algo como

$C + \frac{L}{2}(x-K)$ , y por lo tanto no puede tener límite finito cuando

$x$ tiende a infinito.

Espero que quede más o menos claro, cualquier cosa preguntá de nuevo.
Saludos!