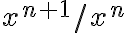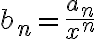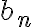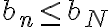CDIVV-2S: Series - Criterio del Cociente (Demostración, Apostol)

Buenas noches, leyendo la demostración de la proposición me surgieron un par de dudas sobre el caso a 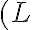$(L$

Primero, no comprendo de dónde sale 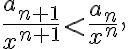$\frac{a_{n+1}}{x^{n+1}} < \frac{a_n}{x^n} ,$

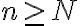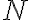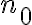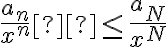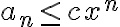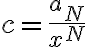Segundo, cuando menciona $n \geq N$ (supongo que $N$ es lo que llamamos $n_0$ ), ¿por qué $\frac{a_n}{x^n} \leq \frac{a_N}{x^N}$ ? Además, trata a esa desigualdad como $a_n \leq c x^{n}$ donde $c= \frac{a_N}{x^N}$ . No entiendo el porqué de eso.

La justificación de que 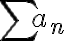$\sum a_n$ esté dominada por una serie convergente, en este caso $\sum x^n$ , la clasifique a ésta como convergente también sí lo entiendo (supongo que es por el criterio de equivalentes)

Re: Series - Criterio del Cociente (Demostración, Apostol)

de Marcelo Fiori - sábado, 2 de septiembre de 2023, 15:39

Hola Alexis,
lo primero sale de escribir

$x$ como

$x^{n+1}/x^n$ , y luego pasar para el otro lado.
Lo segundo es directamente de la observación sobre la monotonía de esa "nueva" sucesión, o sucesión auxiliar

$b_n=\frac{a_n}{x^n}$ .

Como

$b_n$ es decreciente, a partir de ese valor de

$N$ se cumple que

$b_n \leq b_N$ (efectivamente es un "

$n_0$ ")
El final es por el criterio de comparación.

En las notas del curso hay una versión alternativa de esta demostración.

Saludos!