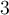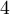Hola Alexis,
Buscamos una sucesión tal que el conjunto de sus puntos de aglomeración sea  , es decir, que haya al menos una subsucesión que converja a
, es decir, que haya al menos una subsucesión que converja a  , al menos una subsucesión que converja a
, al menos una subsucesión que converja a 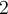 , otra a
, otra a 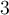 , otra a
, otra a 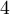 , y que no haya subsucesiones que converjan a otro valor real distinto de esos cuatro.
, y que no haya subsucesiones que converjan a otro valor real distinto de esos cuatro.
En la sucesión que elegiste mostrás correctamente que 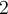 es punto de aglomeración. De hecho sucede que la sucesión converge a
es punto de aglomeración. De hecho sucede que la sucesión converge a 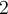 por lo que todas sus subsucesiones convergen a ese valor, por lo que la sucesión no tendrá otros puntos de aglomeración y no nos sirve para la sucesión que buscamos.
por lo que todas sus subsucesiones convergen a ese valor, por lo que la sucesión no tendrá otros puntos de aglomeración y no nos sirve para la sucesión que buscamos.
Avisame si ahora sí está más claro lo que pide el ejercicio y si no te sale o tenés alguna consulta volvés a escribir nomás.
Saludos,
Leandro
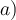
 y vi que, conforme
y vi que, conforme  ,
, 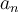 converge a
converge a 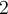 , entonces me tomé la subsucesión
, entonces me tomé la subsucesión  (subsuc. de múltimplos de 2)
(subsuc. de múltimplos de 2)
 sí es punto de aglomeración, pero no sé si esa sea la forma de hacer el ejercicio
sí es punto de aglomeración, pero no sé si esa sea la forma de hacer el ejercicio