Estoy teniendo problemas para entender el límite de esta sucesión. Adjunto lo que pensé que no sé si está bien.
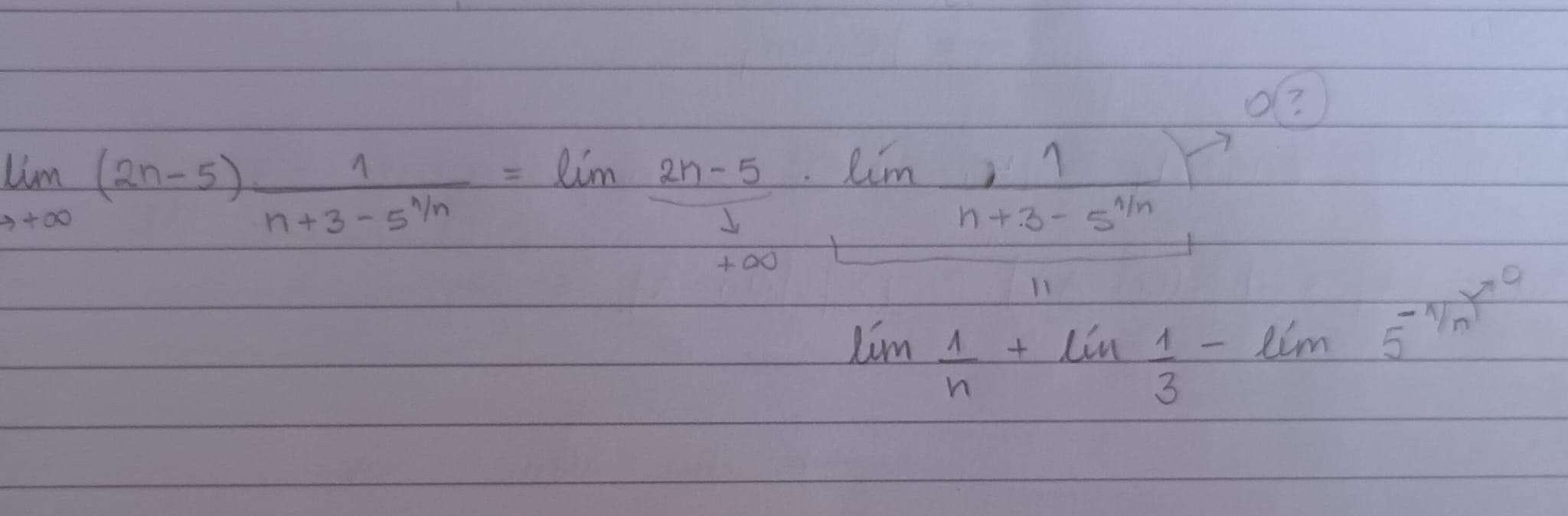
Estoy teniendo problemas para entender el límite de esta sucesión. Adjunto lo que pensé que no sé si está bien.
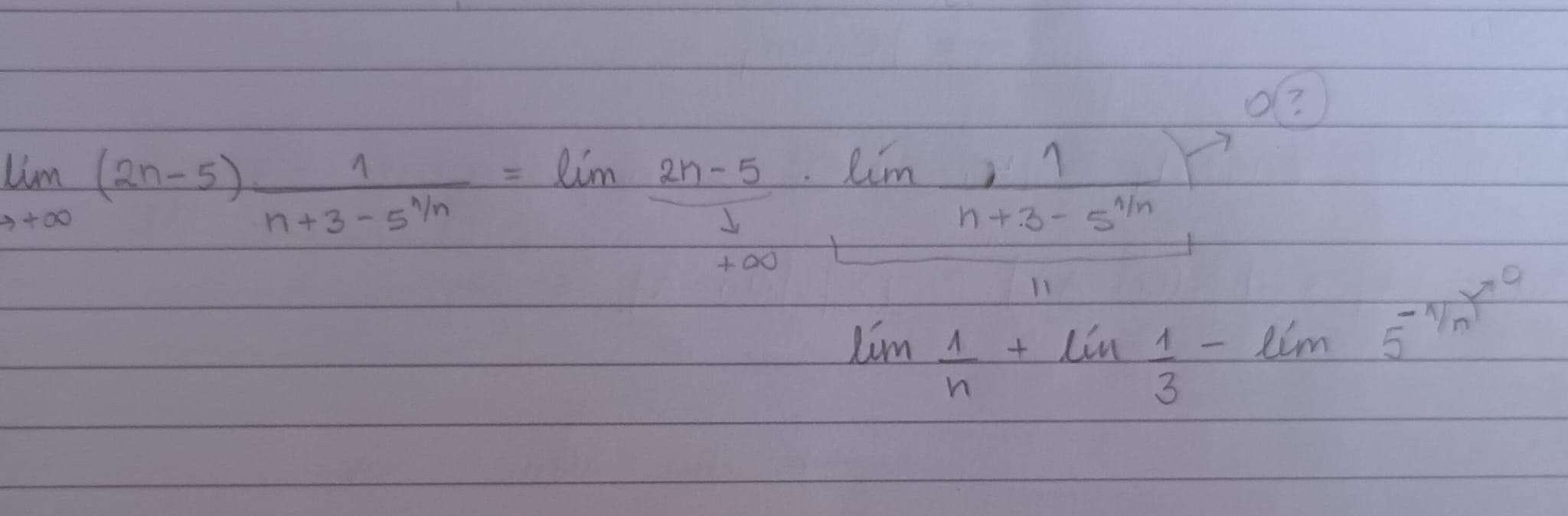
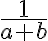 no es igual a
no es igual a 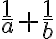 , por lo que no podemos separar el segundo límite en una suma.
, por lo que no podemos separar el segundo límite en una suma.