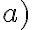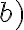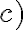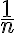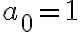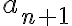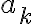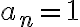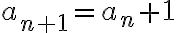Hola, en este ejercicio no logro entender lo de punto de aglomeración, en la parte a logre entender el ejemplo pero en la b no.No entiendo como darme cuenta cual sería la sucesión para que subsucesiones de ella tengan como limite cada natural.
En la parte c, no logro entender por qué 0 no podría ser un punto de aglomeración,si tomamos 1/n como subsucesion,esta tiene limite 0