Sobre la parte 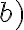 , con escribirla de esa forma alcanza y entender por qué cumple lo pedido. Te comento una forma de definir esa sucesión por recurrencia por si te interesa que sería definir
, con escribirla de esa forma alcanza y entender por qué cumple lo pedido. Te comento una forma de definir esa sucesión por recurrencia por si te interesa que sería definir 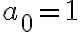 , y para
, y para 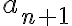 tomar la siguiente regla, si
tomar la siguiente regla, si  es mayor a
es mayor a 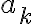 para todos los
para todos los  menores a
menores a  , entonces
, entonces 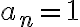 , sino entonces
, sino entonces 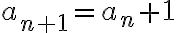 . Esto es, si sos más grande (estrictamente) que todos los valores anteriores entonces volvés a
. Esto es, si sos más grande (estrictamente) que todos los valores anteriores entonces volvés a  , y sino seguís creciendo.
, y sino seguís creciendo.
Sobre la parte , sugeriría que primero pienses en un ejemplo de una sucesión concreta que cumpla que
, sugeriría que primero pienses en un ejemplo de una sucesión concreta que cumpla que 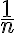 es límite de alguna subsucesión para cada
es límite de alguna subsucesión para cada  (podes usar la parte
(podes usar la parte 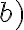 de insumo para construir este ejemplo). Luego observá que
de insumo para construir este ejemplo). Luego observá que  va a ser punto de aglomeración para esta sucesión que pensaste. Finalmente podés ver que el argumento de por qué
va a ser punto de aglomeración para esta sucesión que pensaste. Finalmente podés ver que el argumento de por qué  es punto de aglomeración para esa sucesión en realidad te va a servir para pensar en cualquier sucesión que tenga a
es punto de aglomeración para esa sucesión en realidad te va a servir para pensar en cualquier sucesión que tenga a  incluida en sus puntos de algomeración.
incluida en sus puntos de algomeración.
Saludos,
Leandro
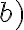 , con escribirla de esa forma alcanza y entender por qué cumple lo pedido. Te comento una forma de definir esa sucesión por recurrencia por si te interesa que sería definir
, con escribirla de esa forma alcanza y entender por qué cumple lo pedido. Te comento una forma de definir esa sucesión por recurrencia por si te interesa que sería definir 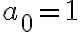 , y para
, y para 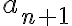 tomar la siguiente regla, si
tomar la siguiente regla, si  es mayor a
es mayor a 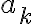 para todos los
para todos los  menores a
menores a  , entonces
, entonces 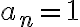 , sino entonces
, sino entonces 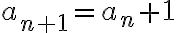 . Esto es, si sos más grande (estrictamente) que todos los valores anteriores entonces volvés a
. Esto es, si sos más grande (estrictamente) que todos los valores anteriores entonces volvés a  , y sino seguís creciendo.
, y sino seguís creciendo. Sobre la parte
 , sugeriría que primero pienses en un ejemplo de una sucesión concreta que cumpla que
, sugeriría que primero pienses en un ejemplo de una sucesión concreta que cumpla que 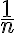 es límite de alguna subsucesión para cada
es límite de alguna subsucesión para cada  (podes usar la parte
(podes usar la parte  de insumo para construir este ejemplo). Luego observá que
de insumo para construir este ejemplo). Luego observá que  va a ser punto de aglomeración para esta sucesión que pensaste. Finalmente podés ver que el argumento de por qué
va a ser punto de aglomeración para esta sucesión que pensaste. Finalmente podés ver que el argumento de por qué  es punto de aglomeración para esa sucesión en realidad te va a servir para pensar en cualquier sucesión que tenga a
es punto de aglomeración para esa sucesión en realidad te va a servir para pensar en cualquier sucesión que tenga a  incluida en sus puntos de algomeración.
incluida en sus puntos de algomeración.Saludos,
Leandro
