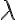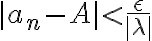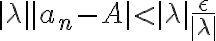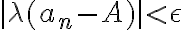Hola, resolví el ejercicio pero solo para el caso que lamb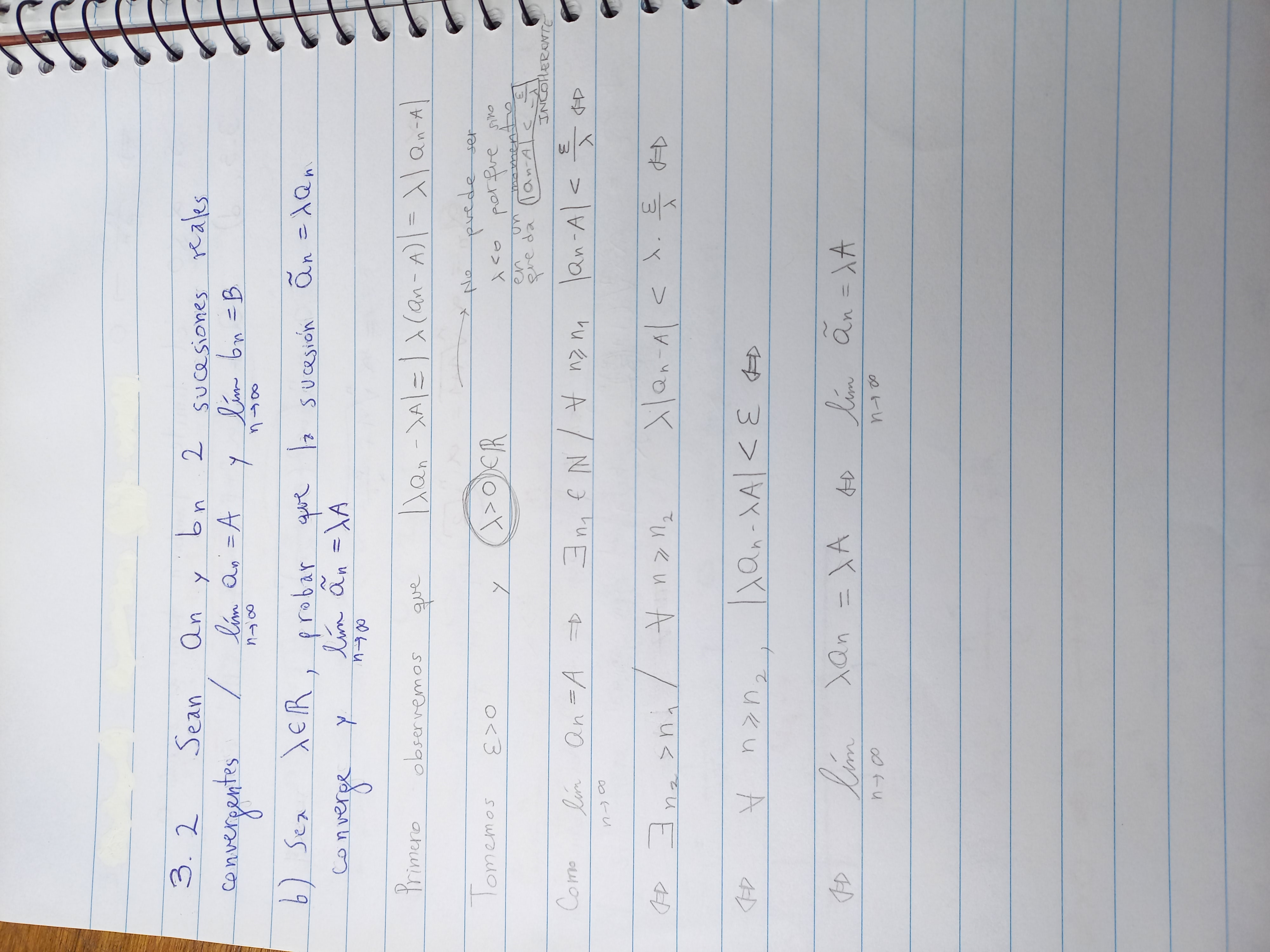 da es positiva.
da es positiva.
Primero, quiero confirmar si lo que hice está bien, y en segundo lugar que me den una idea de cómo hacer para cuando es menor a 0.
Porque imagino que cuando es igual a 0 queda que el límite de 0 cuando n tiende a infinito es 0 y eso es verdad ya de por sí.