Hola buenas, tengo dudas respecto a los ejercicios de demostraciones del practico. Este en particular se me ocurrió como plantearlo pero no estoy seguro. Quería decir que an puede ser cualquier sucesión de la forma x + 1/n con x siendo cualquier real. De esa forma todos los reales serían puntos de acumulación de la función y con eso se podría establecer qué está acotada.
Hola Oscar,
No sé cuál de las dos sentidos estás intentando demostrar. Cuál es tu hipótesis y cuál es tu tesis? Por otro lado, si una sucesión está definida por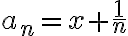
con 
un número real fijo, entonces su límite y único punto de aglomeración es . No sé si es eso a lo que te querés referir en la última sentencia.
Saludos,
Leandro
No sé cuál de las dos sentidos estás intentando demostrar. Cuál es tu hipótesis y cuál es tu tesis? Por otro lado, si una sucesión está definida por
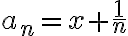con un número real fijo, entonces su límite y único punto de aglomeración es . No sé si es eso a lo que te querés referir en la última sentencia.Saludos,
Leandro
Hola, en principio quería tomar como tesis el sentido contrario, si bn esta acotada entonces f esta acotada. Ahora, esa afirmación qué me colocaste me sirve para probar algo? Era una idea que se me ocurrió, quería saber si podía servir de algo.
Ahora me ubico un poco mejor. No sé a qué te referís con puntos de acumulación de la función, lo que definimos son puntos de acumulación de conjuntos o puntos de aglomeración de sucesiones.