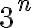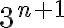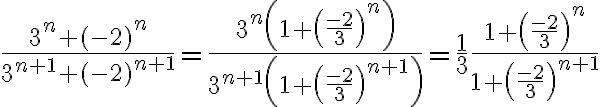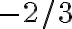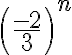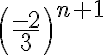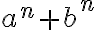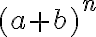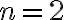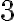P3 - Ejercicio 3.g

P3 - Ejercicio 3.g

de Bruno Capote Hernández -
Número de respuestas: 4
tomar en cuenta solo el "3" arriba y debajo de la división, luego tachar las n es la forma correcta de pensar el ejercicio? da 1/3 como en las soluciones, pero quizás llegué de suerte nomás 
En respuesta a Bruno Capote Hernández

Re: P3 - Ejercicio 3.g

de Pablo Fabian Maurente Sosa -
lo puedes pensar así si
En respuesta a Pablo Fabian Maurente Sosa

Re: P3 - Ejercicio 3.g

de Bernardo Marenco -

Hola. Complementando un poco la respuesta de Pablo, podés pensarlo sacando de factor común un 3^n arriba y un 3^{n+1} abajo, así:

\displaystyle \frac{3^n+(-2)^n}{3^{n+1}+(-2)^{n+1}}=\frac{3^n\left(1+\left(\frac{-2}{3}\right)^n\right)}{3^{n+1}\left(1+\left(\frac{-2}{3}\right)^{n+1}\right)}=\frac13\frac{1+\left(\frac{-2}{3}\right)^n}{1+\left(\frac{-2}{3}\right)^{n+1}}

Como -2/3 tiene valor absoluto menor a 1, tenemos que \left(\frac{-2}{3}\right)^n y \left(\frac{-2}{3}\right)^{n+1} tienden a 0, por lo que ese último cociente tiende a 1.

Saludos
En respuesta a Bernardo Marenco

Re: P3 - Ejercicio 3.g

de Zoé Castro Brando -
Buenas, yo lo resolví haciendo la resta de las bases tanto el el numerador como en el denominador, me queda 1^n/^+n. Como 1 elevado a cualquier número es 1, me queda igual a 1/1, entonces el límite es 1. Por qué esto estaría mal?

En respuesta a Zoé Castro Brando

Re: P3 - Ejercicio 3.g

de Leandro Bentancur -
Hola Zoé,
El error es que a^n +b^n no es igual a (a+b)^n, y lo mismo con la resta. Podés verificarlo para ese caso particular de la sucesión con n=2 o 3 por ejemplo.
Una forma óptima de resolver el ejercicio es la que planteó Bernardo más arriba.
Saludos,
Leandro