Buenas, tengo dudas respecto a este ejercicio. Directamente no se como plantearlo, vi también la solución y no entendí como se llegó a eso. Si me podrían dar un tip de como encararlo, porque me encantaría poder realizarlo.
En respuesta a Oscar Sebastian Núñez Arruda
Re: Práctico 2, Ej 2.1
Intente plantear el volumen de la Bahía en función del tiempo. Coloque un Vo, el volumen medio y le sume un término, el volumen qué variaba con cos(t 2pi/12,5) x el área de la Bahía x altura 1 metro (la altura qué variaba la Bahía)
A eso lo derive y me quedo el flujo, qué es igual a la sección del canal por la velocidad del fluido. De ahí despeje la velocidad qué varía con el tiempo.
A eso lo derive y me quedo el flujo, qué es igual a la sección del canal por la velocidad del fluido. De ahí despeje la velocidad qué varía con el tiempo.
Hola.
Parece estar bien encaminado lo que planteaste. No me queda claro este término que agregaste: "el volumen que variaba con cos(t 2pi/12,5) x el área de la Bahía x altura 1 metro". ¿Qué es esa altura de 1 m? El cos ya corresponde a una altura, por lo que el cos x el área de la bahía ya debería tener unidades de volumen, si multiplicás por otra longitud esto queda mal dimensionalmente.
Saludos.
Parece estar bien encaminado lo que planteaste. No me queda claro este término que agregaste: "el volumen que variaba con cos(t 2pi/12,5) x el área de la Bahía x altura 1 metro". ¿Qué es esa altura de 1 m? El cos ya corresponde a una altura, por lo que el cos x el área de la bahía ya debería tener unidades de volumen, si multiplicás por otra longitud esto queda mal dimensionalmente.
Saludos.
Hola! Con respecto a este ejercicio, tengo una duda tambien. Yo plantie
Variación de volumen = cos ( 2 pi / T * t ) * Area de Bahia
Volumen (t) = integral entre t y 0 de (cos ( 2 pi / T * t ) * Area de Bahia ) + Volumen Inicial = 2 pi / T * sen ( 2 pi / T * t ) * Area de Bahia - 2 pi / T * sen ( 2 pi / T * 0 ) * Area de Bahia + Area de Bahia * h0 = 2 pi / T * sen ( 2 pi / T * t ) * Area de Bahia + Area de Bahia * h0 = ( 2 pi / T * sen ( 2 pi / T * t ) + h0 ) Area de Bahia
velocidad (t) = ( 2 pi / T * sen ( 2 pi / T * t ) + h0 ) Area de Bahia / Area de Solución
Y ahi no se como llegar a la solución
Variación de volumen = cos ( 2 pi / T * t ) * Area de Bahia
Volumen (t) = integral entre t y 0 de (cos ( 2 pi / T * t ) * Area de Bahia ) + Volumen Inicial = 2 pi / T * sen ( 2 pi / T * t ) * Area de Bahia - 2 pi / T * sen ( 2 pi / T * 0 ) * Area de Bahia + Area de Bahia * h0 = 2 pi / T * sen ( 2 pi / T * t ) * Area de Bahia + Area de Bahia * h0 = ( 2 pi / T * sen ( 2 pi / T * t ) + h0 ) Area de Bahia
velocidad (t) = ( 2 pi / T * sen ( 2 pi / T * t ) + h0 ) Area de Bahia / Area de Solución
Y ahi no se como llegar a la solución
Hola Rodrigo.
No me queda claro el razonamiento que seguiste. ¿Qué está integrando? La "variación del volumen" que tenés en la primera línea sería el volumen en un tiempo t, medido respecto al volumen medio, entonces no me queda claro lo que hacés a partir de esta expresión.
Saludos.
No me queda claro el razonamiento que seguiste. ¿Qué está integrando? La "variación del volumen" que tenés en la primera línea sería el volumen en un tiempo t, medido respecto al volumen medio, entonces no me queda claro lo que hacés a partir de esta expresión.
Saludos.
Hola estaba razonando mal, pensando que la integral del caudal es igual a al volumen en el tiempo t desde el punto medio
Integral(Caudal(t)) = AreaLaguna * cos (2 pi / T * t)
Integral(AreaCanal * v(t)) = AreaLaguna * cos (2 pi / T * t)
AreaCanal * Integral(v(t)) = AreaLaguna * cos (2 pi / T * t)
Integral(v(t)) = AreaLaguna / AreaCanal * cos (2 pi / T * t)
v(t) = derivada(AreaLaguna / AreaCanal * sen (2 pi / T * t))
v(t) = AreaLaguna / AreaCanal * derivada( cos (2 pi / T * t))
v(t) = (- 1) AreaLaguna / AreaCanal * (2 pi / T) * sen (2 pi / T * t)
Llego cerca pero me falta la h0 :(
Integral(Caudal(t)) = AreaLaguna * cos (2 pi / T * t)
Integral(AreaCanal * v(t)) = AreaLaguna * cos (2 pi / T * t)
AreaCanal * Integral(v(t)) = AreaLaguna * cos (2 pi / T * t)
Integral(v(t)) = AreaLaguna / AreaCanal * cos (2 pi / T * t)
v(t) = derivada(AreaLaguna / AreaCanal * sen (2 pi / T * t))
v(t) = AreaLaguna / AreaCanal * derivada( cos (2 pi / T * t))
v(t) = (- 1) AreaLaguna / AreaCanal * (2 pi / T) * sen (2 pi / T * t)
Llego cerca pero me falta la h0 :(
Hola.
Sigue sin quedarme claro qué integrás. ¿En qué variable estás integrando?
El ejercicio te da el nivel medio del agua en la bahía en función de t:
, donde 
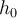es el máximo valor que toma el nivel medio del agua en la bahía.
La velocidad de la superficie del agua en la bahía está dada por la derivada de su posición respecto al tiempo:
.
Finalmente, por continuidad se puede relacionar la velocidad del fluido en la bahía con la velocidad en el canal (la que se pide en la parte a):
.
Saludos.
Sigue sin quedarme claro qué integrás. ¿En qué variable estás integrando?
El ejercicio te da el nivel medio del agua en la bahía en función de t:
, donde 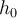es el máximo valor que toma el nivel medio del agua en la bahía.La velocidad de la superficie del agua en la bahía está dada por la derivada de su posición respecto al tiempo:
.Finalmente, por continuidad se puede relacionar la velocidad del fluido en la bahía con la velocidad en el canal (la que se pide en la parte a):
.Saludos.