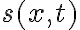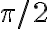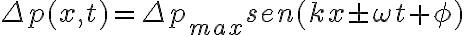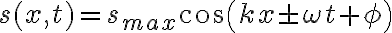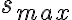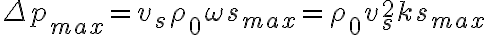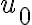En la parte b pide hallar la amplitud de las vibraciones del
aire causadas por este sonido . No sé bien que es está amplitud, en un principio , por equivalencia a ondas en cuerdas, pensé que era lo que multiplica al seno en la ecuación de onda: 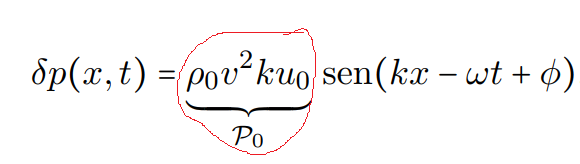
esto es de las notas de clase

Pero la solucion es un sm, con unidades de longitud efectivamente