Buenas
Efectivamente la idea es usar un cambio de variable  y luego usar fracciones simples.
y luego usar fracciones simples.
Como mencionas una vez realizas el cambio de variable te queda dentro de la integral la función 
Una vez tenemos esta función intentamos realizar el método de fracciones simples, ya que es un cociente de polinomios. Pero hay un detalle, para poder separa en dos sumandos de la forma  necesitas que el numerador tenga grado menor que el denominador, y este no es el caso en la expresión
necesitas que el numerador tenga grado menor que el denominador, y este no es el caso en la expresión  .
.
Para conseguir esta relación hay que realizar la división entera de polinomios, o bien realizar algún otro procedimiento (en este ejercicio se puede visualizar fácilmente).
En este caso la división queda  , es decir que
, es decir que 
Intenta ahora encontrar  y
y 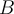 tal que
tal que 
Si tienes dificultades para esto ultimo vuelve a escribir y realizamos la cuenta
Saludos