Hola Zoé, las fórmulas para el resto (ya sea la de Lagrange o la formula integral del resto) las vimos en la última semana de clase. Si por alguna razón te las perdiste podés ver en la Hoja de Ruta de la última semana bibliografía y clases de openfing dedicadas al tema -para esto último la clase 42 sirve-.
Sin embargo, si estás preparando el examen podés no estresarte mucho con este tema pues lo hemos eximido (acá el anuncio) en consideración con la gente que cursó Cálculo DIV el semestre par de 2022, pues no vieron el tema.
Por último, para completar y responder tus preguntas, toda esa estimación del error es porque sabemos que:
-de vuelta, esto es por la fórmula del resto de Lagrange, te recomiendo leas su enunciado-. No sabemos quién es  , pero sabemos que
, pero sabemos que  es
es 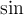 o
o  -dependiendo de
-dependiendo de  , pero las derivadas pares del seno son así-, luego en cualquier caso se tiene que
, pero las derivadas pares del seno son así-, luego en cualquier caso se tiene que  . Por lo tanto
. Por lo tanto
 , pero sabemos que
, pero sabemos que  es
es 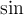 o
o  -dependiendo de
-dependiendo de  , pero las derivadas pares del seno son así-, luego en cualquier caso se tiene que
, pero las derivadas pares del seno son así-, luego en cualquier caso se tiene que  . Por lo tanto
. Por lo tantoy de esa forma sabemos que el resto va a ser menor que 0,001, y por lo tanto, el polinomio de taylor de seno centrado en 0 va a aproximar bien a  en, seguro, las dos primeras cifras decimales.
en, seguro, las dos primeras cifras decimales.
 en, seguro, las dos primeras cifras decimales.
en, seguro, las dos primeras cifras decimales.Saludos,
Bruno


