Hola, estaba leyendo la solución de este ejercicio y me perdí en el momento que se usa Lagrange, no entiendo por qué. Llegué a plantear la aproximación por Taylor y luego no sabría como seguir.

Hola, estaba leyendo la solución de este ejercicio y me perdí en el momento que se usa Lagrange, no entiendo por qué. Llegué a plantear la aproximación por Taylor y luego no sabría como seguir.

Hola Zoé.
El problema pide la segunda cifra decimal de  . Como seno es una función francamente horrible de calcular, justamente aproximarla con un polinomio de Taylor en un punto bonito es una solución sensata (por ejemplo 0, el polinomio de Taylor de seno alrededor de 0 es lindo).
. Como seno es una función francamente horrible de calcular, justamente aproximarla con un polinomio de Taylor en un punto bonito es una solución sensata (por ejemplo 0, el polinomio de Taylor de seno alrededor de 0 es lindo).
El tema es, suponiendo que tenemos un polinomio de taylor 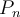 , con
, con  razonablemente grande, ¿cómo sabemos con certeza que
razonablemente grande, ¿cómo sabemos con certeza que  coincide en la segunda cifra decimal con
coincide en la segunda cifra decimal con  ?
?
Ahí es dónde entra la estimación del resto y la fórmula de Lagrange. Sabemos que  . Si queremos que
. Si queremos que  coincida hasta la segunda cifra decimal con
coincida hasta la segunda cifra decimal con  alcanza que
alcanza que  porque en practicamente todos los casos (hay que tener cuidado si la segunda cifra decimal es 0 o 9) esa aproximación es más que suficiente. El problema es que la fórmula de Lagrange -que es una fórmula explicita para el resto- dice
porque en practicamente todos los casos (hay que tener cuidado si la segunda cifra decimal es 0 o 9) esa aproximación es más que suficiente. El problema es que la fórmula de Lagrange -que es una fórmula explicita para el resto- dice
Con  . Buenísimo, pero no nos dice quién es explicitamente
. Buenísimo, pero no nos dice quién es explicitamente 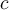 . Ahí es donde entra todo el juego de estimación que hacen en la solución que mostrás.
. Ahí es donde entra todo el juego de estimación que hacen en la solución que mostrás.
En resumen: el polinomio de Taylor te da un valor aproximado a  , la estimación del resto -ya sea usandon la fórmula de Lagrange o la fórmula integral- es lo que te permite decir qué tan buena es la aproximación del valor que te da el polinomio de Taylor.
, la estimación del resto -ya sea usandon la fórmula de Lagrange o la fórmula integral- es lo que te permite decir qué tan buena es la aproximación del valor que te da el polinomio de Taylor.
Espero que esto te haya aclarado un poco el uso del resto, saludos
 , pero sabemos que
, pero sabemos que  es
es 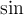 o
o  -dependiendo de
-dependiendo de  , pero las derivadas pares del seno son así-, luego en cualquier caso se tiene que
, pero las derivadas pares del seno son así-, luego en cualquier caso se tiene que  . Por lo tanto
. Por lo tanto en, seguro, las dos primeras cifras decimales.
en, seguro, las dos primeras cifras decimales.