Buenas
Recuerda que la formula de partes dice que, si 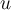 y
y 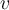 son dos funciones derivables entonces:
son dos funciones derivables entonces:
es decir aparece un menos antes de la integral en la derecha de la igualdad
Por lo que si sustituyes en la formula queda
Cualquier duda vuelve a escribir
Saludos


