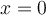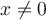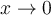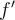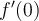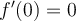CDIV-1S: Primer semestres Segundo Parcial 2019

Buenas tenía una pregunta del ejercicio 3:

Yo pensaba que era la c ya que el límite cuando x tiende a 0 de la funcion da 0, y en x=0 la funcion vale 0 entonces es continua en x=0.

Pero cuando derive la función y le hice el límite cuando x tiende a 0, me queda un coseno(1/x) que es indeterminado, entonces no puedo afirmar que la derivada ahí vale 0 como para que sea derivable.

Por otro lado, para saber si la derivada es continua, se estudia lo de siempre, límites laterales de la función y los igualo a la f´(0) supongo, pero f´(0) no existe entonces sería discontinua la derivada en x=0, si no es así no entendí muy bien que hacer.

Ahora, haciendo la derivada por definición, me da que f´(0) = 0 pero no entiendo por qué no es lo mismo derivar usando regla de la cadena y hacer el límite después.

Re: Primer semestres Segundo Parcial 2019

de Bruno Yemini - martes, 4 de julio de 2023, 11:15

Hola, perdón por la tardanza en responder.

Creo que acá te haces un pequeño enredo entre calcular la derivada de

$f$ en

$x=0$ y la derivada de la expresión

$x^2\sin(1/x)$ , esta última expresión no está definida en 0.

Justamente, si

$x\neq 0$ , la derivada es

$f'(x) = 2x\sin(1/x) + \cos(1/x)$ . Y, como expresas (no muy bien), no existe el límite

$\lim_{x\to 0} \cos(1/x)$ y por lo tanto no tiene límite

$f'(x)$ cuando

$x \to 0$ . En realidad eso te dice en particular que

$f'(x)$ no es continua en

$x=0$ (recordá que para que

$f'$ sea continua tiene que existir ese límite, además de ser igual a

$f'(0)$ .

Ahora, para derivar en 0 no podés usar las reglas de cálculo en

$x^2\sin(1/x)$ porque, justamente, esa expresión no está definida en 0. No nos queda más remedio que usar la definición de derivada. Como dices arriba,

$f'(0) = 0$ . Lo que confirma que:

$f$ es derivable en 0 y

$f'$ no es continua en 0. En definitiva, la opción correcta es la (c).

Hay que tener cierto cuidado al usar las derivadas que nos dan las reglas de cálculo, porque son las derivadas de las expresiones que usamos, si en el punto a derivar la expresión que define la función cambia (por ejemplo, porque estamos en una función definida a trozos), las reglas de cálculo no servirán y tendremos que recurrir a la definición de derivada.

Espero haber aclarado esta duda a ti y a todos los que la tengan, cualquier cosa pregunten.

Saludos

x2sin⁡(1/x)