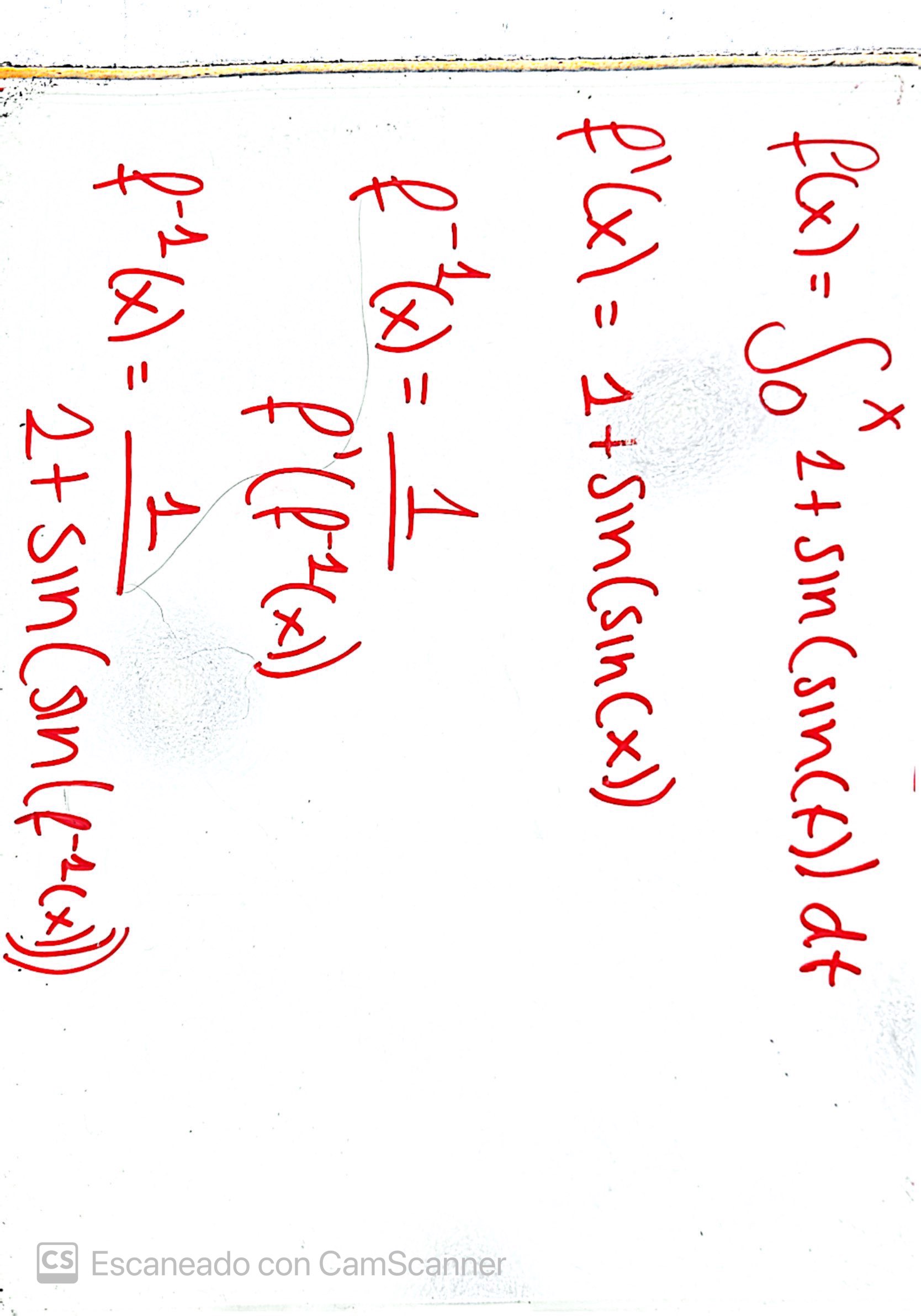Hola, me quedo una duda sobre la última parte, donde tiene ya definido que la derivada de la inversa es 1/f’(f^-1(x))
como sabe que la inversa es X como para sustituir y que le quede la última expresión? Gracias
Hola, me quedo una duda sobre la última parte, donde tiene ya definido que la derivada de la inversa es 1/f’(f^-1(x))
como sabe que la inversa es X como para sustituir y que le quede la última expresión? Gracias

Buenas
No se si entiendo del todo tu consulta
Voy a comentar los últimos pasos y cualquier cosa vuelve a escribir.
De las propiedades anteriores tienes que  . Luego evaluando en
. Luego evaluando en  (es decir tomando
(es decir tomando  ) tienes que
) tienes que
Bien aquí tienes que tener cuidado con la notación  hace referencia a
hace referencia a  , mientras que
, mientras que 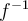 hace referencia a la función inversa de
hace referencia a la función inversa de  y por tanto
y por tanto 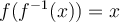 .
.
Juntando todo tenemos que
Como mencione antes no entendí del todo tu duda, por lo que si no era esto vuelve a escribir
Saludos