Hola buenas!, le estaba dando vueltas a este ejercicio y realmente no se me ocurre como concluir el limite de g(x) en mas infinito. Agradecería cualquier tipo de orientación, desde ya muchas gracias!
Segundo Parical-2020-Segundo Semestre-MO6
Número de respuestas: 2
En respuesta a Agustín Marcio Ribeiro García
Re: Segundo Parical-2020-Segundo Semestre-MO6
de Marcos Barrios -
Buenas
La condición relativa a las rectas tangentes te permite concluir que  .
.
Traslademos ese pequeño desfasaje Notemos 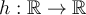 la función
la función  ,
,
Como  para todo
para todo 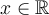 entonces
entonces  difieren en una constante. Es decir existe
difieren en una constante. Es decir existe 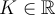 tal que
tal que  por tanto
por tanto
Como  podemos concluir que el limite de
podemos concluir que el limite de  en infinito existe, más precisamente
en infinito existe, más precisamente 
Necesitamos ahora encontrar ese valor de 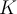 , para eso usaremos la propiedad III
, para eso usaremos la propiedad III
Como  realizando un cambio de variable lineal tenemos que
realizando un cambio de variable lineal tenemos que  . Luego como
. Luego como  tenemos que
tenemos que
Aplicando la propiedad III se tiene que  por tanto
por tanto 
Cualquier cosa vuelve a escribir
Saludos
En respuesta a Marcos Barrios
Re: Segundo Parical-2020-Segundo Semestre-MO6
Buenas!, Muchas gracias por la respuesta. Se entendió!


