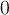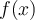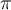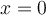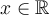Hola, tengo una consulta sobre como se da cuenta que tiene que evaluar las raices solo en [-1,1] porque antes dice que la funcion siempre va a ser menor a uno pero nunca dice porque no toma un intervalo hasta menos infinito
además, para darme cuenta si es un mínimo relativo o absoluto, tengo que tomarme un entorno en el mínimo y fijarme si los f(x) son todos mayores a f(minimo)? gracias


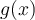


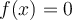


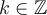

![[-1,1] [-1,1]](https://eva.fing.edu.uy/filter/tex/pix.php/d060b17b29e0dae91a1cac23ea62281a.png)