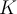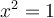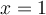Buenas, quería consultar por qué el 1 sería verdadero y el 5 falso.
Hola Santiago.
En 5), como T es unitario tenemos que , y como T es autoadjunto tenemos
, y como T es autoadjunto tenemos 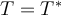 , de donde
, de donde  y por tanto
y por tanto  .
.
En 5), como T es unitario tenemos que
 , y como T es autoadjunto tenemos
, y como T es autoadjunto tenemos 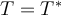 , de donde
, de donde  y por tanto
y por tanto  .
.Esto no implica que T=Id, como contrajemplo considera la matriz 2 x 2 cuya primera columna es (-1,0) y la segunda columna es (0,-1).
En 1), al ser un EV sobre los complejos, si asumimos dimensión finita, todas las raíces del polinomio característico serán valores propios.
Si trabajamos en una base ortonormal B y llamamos M a la matriz asociada a T, tendremos que la matriz asociada a 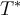 es
es  .
.
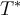 es
es  .
.Llamemos  , entonces
, entonces  (hemos usado que conjugar y transponer conmutan y que conjugar dos veces devuelve la misma matriz, así como transponer dos veces, que el conjugado de un producto es el producto de los conjugados y que la transpuesta de un producto es el producto de las transpuestas en orden inverso).
(hemos usado que conjugar y transponer conmutan y que conjugar dos veces devuelve la misma matriz, así como transponer dos veces, que el conjugado de un producto es el producto de los conjugados y que la transpuesta de un producto es el producto de las transpuestas en orden inverso).
 , entonces
, entonces  (hemos usado que conjugar y transponer conmutan y que conjugar dos veces devuelve la misma matriz, así como transponer dos veces, que el conjugado de un producto es el producto de los conjugados y que la transpuesta de un producto es el producto de las transpuestas en orden inverso).
(hemos usado que conjugar y transponer conmutan y que conjugar dos veces devuelve la misma matriz, así como transponer dos veces, que el conjugado de un producto es el producto de los conjugados y que la transpuesta de un producto es el producto de las transpuestas en orden inverso).Entonces la matriz A es hermítica y por tanto el operador  es diagonalizable, y por tanto también lo es el operador
es diagonalizable, y por tanto también lo es el operador  .
.
 es diagonalizable, y por tanto también lo es el operador
es diagonalizable, y por tanto también lo es el operador  .
.Saludos
J.
Gracias! Pero no termino de entender por qué aunque T es igual a T inversa no se puede decir que T es la identidad (pensándolo con matrices asociadas), y por que T a la 2 sí lo es
Saludos
J.