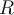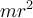Buen día, no entiendo por qué la respuesta es esta:
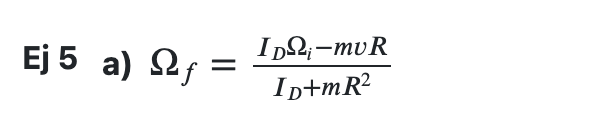
O sea, el término del numerador lo entiendo, pero en el denominador, ¿por qué es Id + mR^2?
Cuando el plato se detiene supongo que el momento angular final sería el del disco más la masa del insecto pero no veo de dónde sale el R^2