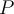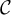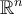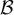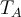Hola, queria consultar el metodo para obtener la matriz P que cumple que la inversa de P es P transpuesta, o P transpuesta inverasa en el caso complejo.
¿Luego de hayar los vecotres propios, debo normalizarlos, y al colgarlos en una matriz esa seria la matriz P?