[Ejercicio 3][Parte B]

[Ejercicio 3][Parte B]

de Thiago Caetano Acuña Vinoles -
Número de respuestas: 2

Buenas! Me surgieron algunas dudas haciendo este ejercicio.

Primero que nada la gramática 2 fue la única que encontré regular. De hecho regular extendida. Y no sé si hay otras.

Luego, a la hora de encontrar el grafo, lo hice bastante a ojo ya que lo único que encontré en el teórico fue que en las notas se comenta cómo sería el pasaje de una Grmática Regular (tanto izquierda como derecha, en este caso derecha) a un Autómata Finito; pero no dice nada sobre gramáticas regulares extendidas. 
Entonces lo que hice fue: tomar la gramática simplificada, transformar las variables en estados, siendo q_0=S , agregar las transiciones derivadas de las reglas "más directas" como S\rightarrow bB  o  A\rightarrow b , etc. Y luego agregar nodos y transiciones a ojo para modelar las restantes reglas.

No estoy seguro si este era el objetivo del ejercicio.


La gramática simplificada de la cual me basé para construir el autómata fue:

S\rightarrow abS|bbaA|bB|b\\ A\rightarrow bbaA|bB|b\\ B\rightarrow bbb

Y el Autómata Finito resultante me quedó:


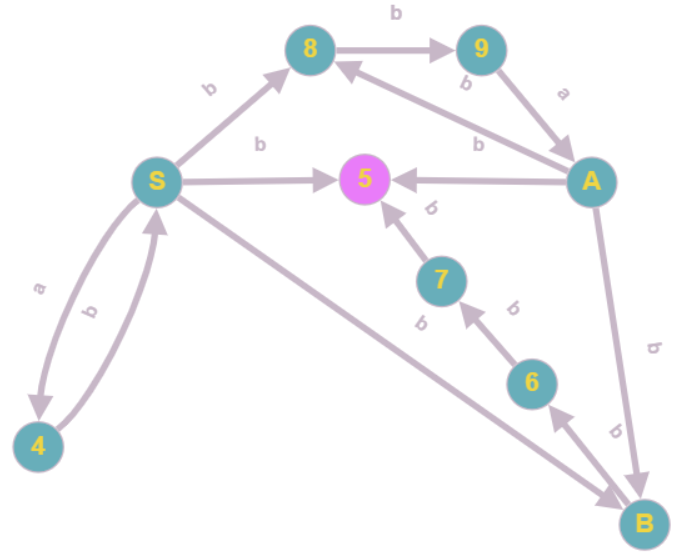
Siendo S,A,B los estados equivalentes a las variables, 4,5,6,7,8,9 estados "auxiliares" y  F=\{5\}.
En respuesta a Thiago Caetano Acuña Vinoles

Re: [Ejercicio 3][Parte B]

de Santiago Gongora -
Buenas tardes Thiago,

no sé si chequeaste este hilo donde hablamos de este mismo ejercicio; en el último mensaje comento algo muy relacionado con tu consulta :)

Este tema es mencionado a veces por Juanjo en el teórico, pero es uno de esos que solemos dejar para trabajar en el práctico, puesto que la correspondencia es sencilla de entender. De hecho, luego de comprender la definición de gramática lineal derecha ya el paralelismo con el AF surge inmediatamente, como me parece que te pasó a vos también.

Miré por arriba el autómata y la gramática que mostrás y a simple vista parece que se corresponden. De hecho, yo no veo que hayas hecho nada "a ojo", sino un procedimiento bastante claro:

  • cada variable se asocia a un estado
  • las reglas donde se produce un símbolo terminal y cero o una variable (tipo S \longrightarrow bB) se "traducen" directamente en una transición con ese símbolo
  • para las reglas donde se produce una tira de terminales y cero o una variable (tipo S \longrightarrow bbaA) se necesita más de un estado (que vos los etiquetas con números) para hacer ese camino.
Lo que obtenés de esa forma, que es lo esperado, es un autómata finito no determinista. Si quisieras un autómata más "elegante" basta con hacerlo determinista y minimizarlo (cosa que no se pide).

Cualquier cosa a las órdenes,
Santi

PD: Cuando antes hablé de comprender la definición de Gramática Lineal Derecha, me refería sobre todo a notar que como las invocaciones a variables están siempre del lado derecho y puede haber como máximo 1 por regla, entonces el poder expresivo (y de cómputo) de esas gramáticas es totalmente equivalente al de cualquier autómata finito