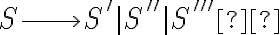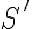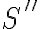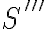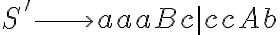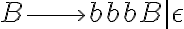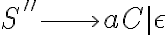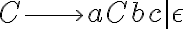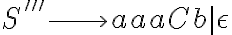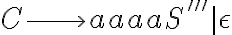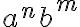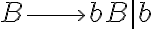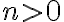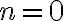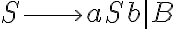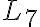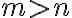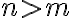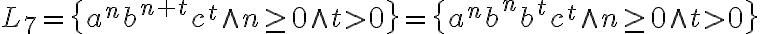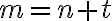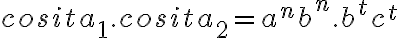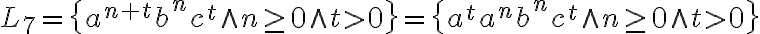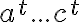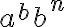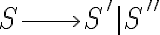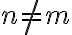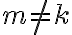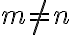Buen día Thiago,
disculpá la demora en responder; al postergarse el parcial, la corrección se nos solapó con el cronograma de las clases y estamos al re palo :P
Voy por partes, para señalizar bien las diferentes dudas (y facilitarte la lectura).
Separar en casos
Lo primero que quiero confirmarte es que vas por el camino correcto. La idea es que puedan separar el problema en casos de alguna manera disjuntos, como hiciste, donde la solución de uno sea totalmente separada a la solución de los otros. Luego el pique para unir todo es usar una regla inicial  que te deje elegir al inicio cuál caso es el que vas a generar. O sea, algo como
que te deje elegir al inicio cuál caso es el que vas a generar. O sea, algo como 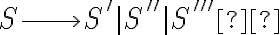 , donde
, donde 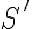 sería la variable de inicio del "camino" para el caso 1,
sería la variable de inicio del "camino" para el caso 1, 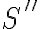 sería la variable de inicio del "camino" para el caso 2 y
sería la variable de inicio del "camino" para el caso 2 y 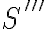 sería la variable de inicio del "camino" para el caso 3.
sería la variable de inicio del "camino" para el caso 3.
Así que luego vas a tener reglas para cada una de las """"subgramáticas"""" que arrancan con esos símbolos iniciales, tipo (va frutazo):
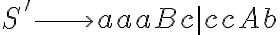
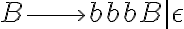
y
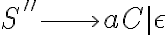
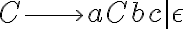
y
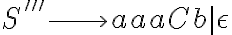
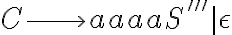
Pique para generar cantidades desiguales
Sobre cómo generar
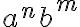
con
n<m , el pique es hacer básicamente lo que vos hiciste. A mi en general me queda práctico hacer algo así:

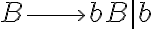
Es decir, primero se genera la cantidad "igual" de a y b, y luego con la variable B se generan solo las b que provocan la desigualdad.
La anterior gramática asume que 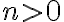 , puesto que no se da paso a la variable B a no ser que se ponga un par de a-b. Si el lenguaje te dijera que se puede dar el caso donde
, puesto que no se da paso a la variable B a no ser que se ponga un par de a-b. Si el lenguaje te dijera que se puede dar el caso donde 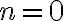 , entonces hacemos este cambio:
, entonces hacemos este cambio:
permitiendo dar paso a la variable B sin obligar un par a-b.
La estrategia que sigue este caso es el de tener dos partes del lenguaje que se concatenan. Fijate si con ese pique podés escribir una gramática que genere dos cositas que concatenes: 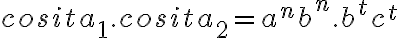 .
.
En el caso 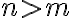 ahora vas a poder reescribir el lenguaje como:
ahora vas a poder reescribir el lenguaje como: 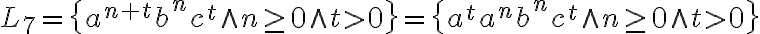 .
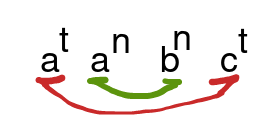
. La estrategia de este caso es la de generar cosas anidadas (la fortaleza principal de las gramáticas libres de contexto). Fijate que pasa algo así:
donde la dependencia en rojo está "más afuera" que la dependencia en verde. Por la naturaleza recursiva de las GLCs, la estrategia es siempre generar de más afuera a más adentro. Así que el pique acá es que generes primero la dependencia 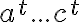 y luego la del centro
y luego la del centro 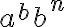 .
.
Como te imaginarás, este pique escala bien con lenguajes más grandes: primero se generan las dependencias de las puntas y luego se va modelando hacia el centro.
Parte 9
Con todo lo anterior, esta gramática es bastante más fácil. Esta la podés dividir en 4 casos como hiciste, o simplemente podés dividirla en dos:
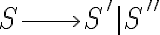
donde
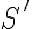
arranca la """subgramática""" que genera el caso
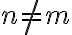
y
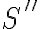 arranca la """subgramática""" que genera el caso
arranca la """subgramática""" que genera el caso 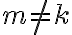 .
.
Fijate que lo que puse bajo el título "Pique para generar cantidades desiguales" es para el caso donde hay una variable que es la que seguro crece más que la otra; o sea, m>n o m<n. Sin embargo, si lo pensás un toquecito vas a ver que se te ocurre cómo modificar ese pique para hacerlo más general y poder modelar algo del estilo 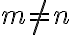 . No te lo spoileo así hacés el razonamiento.
. No te lo spoileo así hacés el razonamiento.
Resumen de los tres piques máximos
Los tres piques que siempre tienen que tener en mente son:
- Muchas veces el lenguaje se puede reescribir con otras variables para que todo quede como la concatenación de dos o más lenguajes.
- Muchas veces el lenguaje se puede reescribir con otras variables para que todo quede expresado con dependencias anidadas.
- Las gramáticas nos permiten separar en casos. Esto puede darse tanto desde el inicio de
la gramática con la variable S, como también más adentro con otras variables (por
ejemplo si el análisis por casos se da en una parte "más interior" en la recursión de la
gramática).
Fin (siiiiuuuu)
Bueno, creo que abordé todas las dudas que planteaste. Pero porfa volvé a preguntar por cualquier parte de esta biblia, o de otras dudas que te vengan relacionadas.
Saludo y vamo arriba con eso,
Santi
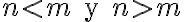 . Pero no logro ver como hacer que la cantidad de
. Pero no logro ver como hacer que la cantidad de  sea exactamente esa diferencia.
sea exactamente esa diferencia.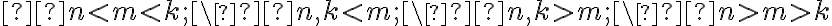 pero no logro unirlo todo.
pero no logro unirlo todo.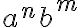 con
con  estaba usando:
estaba usando: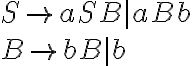 (O algo análogo si es
(O algo análogo si es  )
)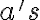 y
y 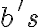 para el 7 y una idea de como unir las cosas en el 9.
para el 7 y una idea de como unir las cosas en el 9.