[Ejercicio 3] [Parte B] [Parte 2]

[Ejercicio 3] [Parte B] [Parte 2]

de Santiago Agustín Silveira Pérez -
Número de respuestas: 7

Hola.

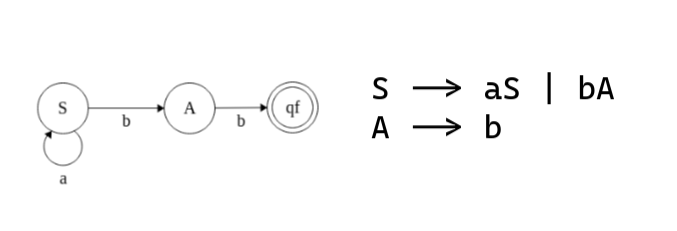
Estoy bastante trancado con este en particular (el de a lo sumo dos b). El hecho de que las b's puedan estar al
principio, al final, en medio, una mezcla, que puedan estar o no, me confunde bastante a la hora de elaborar una
solución y que quede regular. Podrían darme algunas pautas para encararlo?

Saludos.

Santiago.


En respuesta a Santiago Agustín Silveira Pérez

Re: Ejercicio 3, parte B, 2

de Santiago Gongora -

Buenas tardes Santiago ¿cómo estás? :)

Para este ejercicio lo que te recomiendo es que pienses primero en el autómata finito que reconoce ese lenguaje regular.

Como estuvimos viendo en la clase de consulta de hoy, hay un fuert(ísimo) paralelismo entre las gramáticas regulares y los autómatas finitos. Los símbolos variables de una gramática regular se comportan similar a los estados del AF, y los símbolos terminales similar a las transiciones del AF.



Este pique de pensar primero el AF te lo recomiendo también para el L_2 de la parte C de este mismo ejercicio, que está medio complicado de pensar directamente en la gramática. El concepto de equivalencia lo vas a usar también en el ejercicio 4 parte B y en el ejercicio 7.

Cualquier cosa volvé a preguntar :)

Saludos,
Santi
En respuesta a Santiago Gongora

Re: Ejercicio 3, parte B, 2

de Alberto Gaetano Di Russo De Lima -
Hola, buenas noches. Me quedó una duda con respecto al pasaje de AF a gramática regular.
1) Si consideramos un estado X, el cual es estado final, sería correcto poner: X -> epsilon ?
2) En el caso que pusiste como ejemplo, la regla de producción S -> bA se genera ya que desde S, leyendo "a", paso al estado A. Pero como sería en el caso que la gramática fuera lineal derecha, puedo usar el mismo autómata pero interpretandolo de otra forma? Lo mismo para el caso del ejercicio 4, parte B, que en un momento hay que interpretar por ejemplo S -> aSb, como se representaría en un autómata?
Te agradecería algún ejemplo.
Gracias, saludos.
En respuesta a Alberto Gaetano Di Russo De Lima

Re: Ejercicio 3, parte B, 2

de Santiago Gongora -
Buen día Alberto,

mencionás varios conceptos en el mensaje así que voy a ir por partes.

1) X \longrightarrow \epsilon


Sí, si X es un estado final, entonces está muy bien poner la producción X \longrightarrow \epsilon .

Esto viene dado porque al ser X un estado de aceptación, no "necesita" consumir otro símbolo de la entrada para aceptarla. Análogamente, la gramática no "necesitaría" generar otro símbolo terminal para que sea una tira correcta.

El caso de borde en el que podemos pensar es cuando \epsilon pertenece al lenguaje aceptado por el autómata. En ese caso el estado inicial q_0 va a ser final, por lo que tendría todo el sentido que el símbolo inicial de la gramática pudiera generar \epsilon. Así que, nuevamente, vemos que sería adecuado tener la producción S \longrightarrow \epsilon .


2) Paralelismo entre AF-GramRegular pero con las variables "en el otro lado"


Cuidado que escribiste "cómo sería en el caso que la gramática fuera lineal derecha". Acordate que es lineal derecha si para todas las reglas se cumple que el símbolo no terminal aparece siempre a la derecha de la regla (por ejemplo S \longrightarrow aabX | aaab | X ); análogamente es lineal izquierda si el símbolo aparece siempre a la izquierda de la regla (por ejemplo S \longrightarrow Xaab | aaab | X ).

Así que la duda que tenés es respecto a la gramática lineal izquierda.

La respuesta a tu pregunta "puedo usar el mismo autómata pero interpretandolo de otra forma?" es sí. La forma de pensarlo ahora es partiendo desde los estados finales y pensando en "qué estado se estaba para que el símbolo que fue consumido provocara una transición al actual estado". Por ejemplo, para el siguiente fragmento de autómata, donde se ven dos estados (H y G) que sirven de estados previos a uno final (J)

la regla para J quedaría: J \longrightarrow H b | G a | J a.

Vas a ver que luego de hacer un ejercicio y chequear que la gramática te haya quedado bien, vas a entender mucho mejor cómo se da el paralelismo. Esto paralelismo (Gramática regular izquierda y AF) lo vas a necesitar para el la parte 2 del ejercicio 7.


3) S \longrightarrow aSb


Al final de tu mensaje consultás sobre esta producción en particular y cómo modelarla con un autómata. El lenguaje generado por esa gramática no puede ser reconocido por un AF porque la gramática no es regular. Fijate que esa regla no cumple con la definición de gramática regular (ver este hilo) porque la invocación a un símbolo variable (o no terminal) no está en uno de los extremos: no aparece ni a la derecha ni a la izquierda, sino que aparece en el medio de una cadena de terminales.

Este comportamiento, de poner símbolos en medio de otros símbolos, rompe con la linealidad que caracteriza a los autómatas finitos, de leer la entrada secuencialmente. De ahí el nombre de las gramáticas regulares: gramática lineal izquierda y gramática lineal derecha.

Así que la respuesta, de nuevo, es que el lenguaje generado por  la gramática que contiene a la regla S \longrightarrow aSb no puede ser reconocido por un autómata finito.


________________________________________________________________________

Espero haya quedado todo un poco más claro. Pero en caso contrario, por favor, volvé a consultar :)

Saludos,
Santi
En respuesta a Santiago Gongora

Re: Ejercicio 3, parte B, 2

de Santiago Agustín Silveira Pérez -
Me salió aplicando esa idea, muchas gracias!!!
En respuesta a Santiago Agustín Silveira Pérez

Re: Ejercicio 3, parte B, 2

de Santiago Gongora -
Ah demás :)

Cualquier cosa, a las órdenes, como siempre.

Saludos,
Santi
En respuesta a Santiago Gongora

Re: Ejercicio 3, parte B, 2

de Alberto Gaetano Di Russo De Lima -
Santiago, quedó muy claro si.
La última duda sería el caso en el que se deba consumir más de una tira del lenguaje, por ejemplo, en el caso que modelar X -> aaY, lo tendría que hacer con una transición, de tal forma que, desde un estado X, consumiendo la tira “aa”, paso al estado Y?
Gracias.
En respuesta a Alberto Gaetano Di Russo De Lima

Re: Ejercicio 3, parte B, 2

de Santiago Gongora -

Buenas tardes,

buenísimo que haya quedado más claro :D

Ojo, creo que a lo que te referís no es "más de una tira del lenguaje" sino "más de un símbolo del alfabeto". Te estás refiriendo al caso donde una producción de la gramática regular contiene más de un símbolo terminal, como el caso que mencionás: X \longrightarrow aaY, con \Sigma=\{a,b\}.
Y cuidado que las funciones de transición \delta de los autómatas no están definidas para tiras, sino para símbolos. No se puede hacer lo que comentás, de consumir "aa". Así que en ese caso, tendrías algo como:



donde "aux" es un estado que no se corresponde a una símbolo variable de la gramática regular, sino que sirve para realizar el paralelismo entre la gramática y el autómata.

Saludos,
Santi