Sistemas no conservativos preintegrables (notas pág. 47)

Sistemas no conservativos preintegrables (notas pág. 47)

de Juan Agustín Rivero Szwaicer -
Número de respuestas: 2

Buenas, en el ejemplo que se da en las notas comienza aplicando 2da ley en dirección 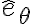\hat{e}_{\theta} y por lo que entendí, como no hay fuerzas residuales en esa dirección puede llegar a algo de la forma \ddot{\theta}+f(\theta)=0, pero si hueran fuerzas residuales, ¿no se podría llegar también a algo como eso?

Tampoco entiendo a lo que le llama "ecuación del sistema".
En respuesta a Juan Agustín Rivero Szwaicer

Re: Sistemas no conservativos preintegrables (notas pág. 47)

de Florencia Benitez Martinez -
Hola Agustín,
lo que dice es que no hay una fuerza reactiva. Se refiere a que no hay fuerza de rozamiento, debido a que la guía es lisa.
En caso de haber fuerzas residuales en esa dirección, se llegará a una ecuación con una fuerza desconocida (por ejemplo, la normal). 
Esto significa que necesitaríamos de una segunda ecuación para obtener la ecuación de movimiento del sistema.
Saludos!
En respuesta a Florencia Benitez Martinez

Re: Sistemas no conservativos preintegrables (notas pág. 47)

de Juan Agustín Rivero Szwaicer -
Ah, okey, creo que entendí. Lo que me dices es que para esa fuerza desconocida no puedo expresarla en función de tita (porque depende de más cosas, por ejemplo la velocidad de la guía), por lo que no puedo plantear una ecuación (diferencial) que solamente dependa de tita. ¿Sería eso?
Saludos