Buenas
Primero utilizando la propiedad del limite del producto (Proposición 31 de las notas de Límite- Ejercicio 4.2-4.e) puedes ver que
La idea ahora es usar la propiedad 30 de las notas "acotado por 0".
La función 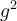 esta acotada en un entorno de 0 pues tiene limite finito (Proposición 29 de las notas de Límite) De donde se deduce que
esta acotada en un entorno de 0 pues tiene limite finito (Proposición 29 de las notas de Límite) De donde se deduce que  también esta acotada.
también esta acotada.
Luego como  esta acotada en un entorno de 0 y
esta acotada en un entorno de 0 y 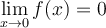 se tiene que
se tiene que 
Saludos
