Buenas tenia una duda acerca de como quedaría el bosquejo grafico de esta función:
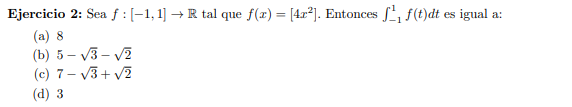
Buenas tenia una duda acerca de como quedaría el bosquejo grafico de esta función:
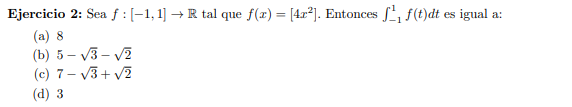
Buenas
Primero que nada la función que se pide integrar es parte entera de  , lo que en nuestro curso notamos como
, lo que en nuestro curso notamos como  . Lo aclaro por que nosotros estuvimos usando la notación [] para la distancia al entero mas cercano.
. Lo aclaro por que nosotros estuvimos usando la notación [] para la distancia al entero mas cercano.
Para entender el gráfico de la función  , hay que entenderlo como una composición (continuo con la explicación luego del gráfico)
, hay que entenderlo como una composición (continuo con la explicación luego del gráfico)

Como puedes ver la función  es escalonada, por lo que para calcular la integral tendrás que averiguar los puntos marcados sobre el eje
es escalonada, por lo que para calcular la integral tendrás que averiguar los puntos marcados sobre el eje 
Veamos primero los 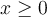 (la parte negativa es análoga)
(la parte negativa es análoga)
Si  quiere decir que
quiere decir que  verifica
verifica  o lo que es lo mismo
o lo que es lo mismo  .
.
Calcular  puede ser difícil en general, pero en este caso no. Ya que
puede ser difícil en general, pero en este caso no. Ya que  es monótona creciente (en
es monótona creciente (en 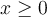 ) y tiene como imagen
) y tiene como imagen 
En esta situación se cumple que  , es decir que debes calcular la preimágen de los naturales. Puedes interpretarlo en el grafico que como g "va creciendo" lo que tienes que detectar es cuando
, es decir que debes calcular la preimágen de los naturales. Puedes interpretarlo en el grafico que como g "va creciendo" lo que tienes que detectar es cuando  pasa por un natural, (corta una recta de la forma
pasa por un natural, (corta una recta de la forma  ).
).
Vamos con los primeros casos  ,
,  (esto ultimo se deduce de resolver
(esto ultimo se deduce de resolver  con
con 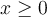 ).
).
Intenta terminar el ejercicio desde aquí y cualquier cosa vuelve a escribir
Saludos