CDIV-1S: Ejercicio 3 Primer parcial S.S 2020

Hola, Tengo una duda sobre este ejercicio, la respuesta correcta es la A pero no entiendo porque la función no es inyectiva si todos los valores que van de [0,2] les corresponde una imagen diferente
Muchas Gracias.

Re: Ejercicio 3 Primer parcial S.S 2020

de Juan Pablo Borthagaray - jueves, 13 de abril de 2023, 08:14

Hola Guzman,

Ese ejercicio sale aplicando los teoremas de Bolzano y de Weierstrass (para la no inyectividad y la no sobreyectividad, respectivamente).

En las clases de teórico de mañana vamos a empezar a hablar de estos teoremas. El ejercicio de práctico (5.1.3) que mencionó Marcos en el aviso que mandó ayer va justamente en la misma línea que este ejercicio sobre el que preguntás.

Re: Ejercicio 3 Primer parcial S.S 2020

de Zoé Castro Brando - lunes, 1 de mayo de 2023, 08:56

Hola, como se aplicarían los teoremas al ejercicio? No entiendo. Yo llegué a la conclusión de que nunca es inyectiva porque sube a cuatro y después baja a 3, pero no entiendo por qué no puede ser sobreyectiva. Puse la respuesta C y no entiendo por qué está mal.

Re: Ejercicio 3 Primer parcial S.S 2020

de Marcos Barrios - lunes, 1 de mayo de 2023, 15:39

Buenas

El ejercicio plantea funciones continuas con dominio $[0,2]$ por tanto, por Weierstrass tienen que tener máximo y mínimo.

Sea $f:[0,2] \to (0,5)$ continua, por Weierstrass f tiene máximo y mínimo, notemos $a = \min\{f(x) : x \in [0,2]\}$ , $b = \max\{f(x) : x \in [0,2]\}$ .

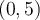Como el codomino de $f$ es $(0,5)$ entonces $a \in (0,5)$ y $b\in (0,5)$ . Es decir $0< a \leq b < 5$

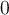En particular $p = \frac{a}{2}$ verifica que $0$ (es decir esta en el intervalo 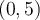$(0,5)$ ) y no esta en la imagen de $f$ (pues es menor al mínimo) por tanto $f$ no puede ser sobreyectiva.

En esencia el ejercicio dice que la imagen de esta función no puede ser un intervalo abierto.

Saludos